Απειροστή Περιστροφή

Απειροστική Περιστροφή

Infinitesimal rotations, Infinitesimal Rotation

Απειροστικός Μετασχηματισμός

Μετασχηματισμός
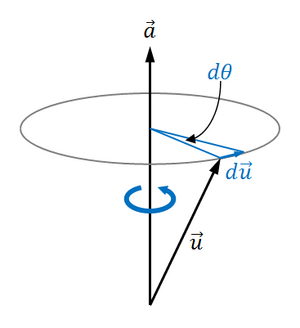
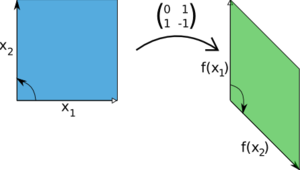
Σημειακός Μετασχηματισμός
Συνεχής Μετασχηματισμός
Διακριτός Μετασχηματισμός
Χρονική Αναστροφή
Χωρική Αναστροφή
Χρονική Μεταφορά
Χωρική Μεταφορά
Χρονική Στροφή
Χωρική Στροφή
Αβελιανός Μετασχηματισμός
Αναβελιανός Μετασχηματισμός
Γαλιλαϊκός Μετασχηματισμός
Μετασχηματισμός Lorentz
Μετασχηματισμός Poincare

Μετασχηματισμός
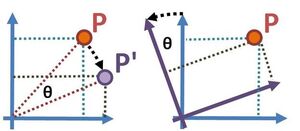
Ενεργητικός Μετασχηματισμός
Παθητικός Μετασχηματισμός
Μετασχηματισμός Στροφής

Χωρική Στροφή

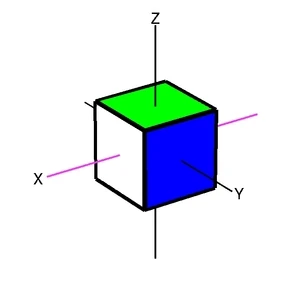
- Ένας μετασχηματισμός.

Ετυμολογία

Η ονομασία "Απειροστικός" σχετίζεται ετυμολογικά με την λέξη "άπειρο".

Εισαγωγή

The matrix exponential of a skew-symmetric matrix $A$ is then an orthogonal matrix $R$:

$R = \exp(A) = \sum_{n=0}^\infty \frac{A^n}{n!}.$

The image of the exponential map of a Lie algebra always lies in the connected component of the Lie group that contains the identity element. In the case of the Lie group $O(n),$ this connected component is the special orthogonal group $SO(n),$ consisting of all orthogonal matrices with determinant 1. So $R = \exp(A)$ will have determinant +1.

Moreover, since the exponential map of a connected compact Lie group is always surjective, it turns out that every orthogonal matrix with unit determinant can be written as the exponential of some skew-symmetric matrix.

In the particular important case of dimension $n=2,$ the exponential representation for an orthogonal matrix reduces to the well-known polar form of a complex number of unit modulus.

Indeed, if $n=2,$ a special orthogonal matrix has the form

$\begin{bmatrix} a & -b \\ b & \,a \end{bmatrix},$

with $a^2 + b^2 = 1$.

Therefore, putting $a = \cos\theta$ and $b = \sin\theta,$ it can be written

${\begin{bmatrix}\cos \,\theta &-\sin \,\theta \\\sin \,\theta &\,\cos \,\theta \end{bmatrix}}=\exp {\begin{bmatrix}0&-\theta \\\theta &\,0\end{bmatrix}}$

which corresponds exactly to the polar form $\cos \theta + i \sin \theta = e^{i \theta}$ of a complex number of unit modulus.

Απόδειξη

${\begin{aligned}e^{i\theta }&=1+ix+{\frac {(i\theta )^{2}}{2!}}+{\frac {(i\theta )^{3}}{3!}}+{\frac {(i\theta )^{4}}{4!}}+{\frac {(i\theta )^{5}}{5!}}+\cdots \\[8pt]&=1+i\theta -{\frac {\theta ^{2}}{2!}}-{\frac {i\theta ^{3}}{3!}}+{\frac {\theta ^{4}}{4!}}+{\frac {i\theta ^{5}}{5!}}+\cdots \\[8pt]&=\left(1-{\frac {\theta ^{2}}{2!}}+{\frac {\theta ^{4}}{4!}}-\cdots \right)+i\left(x-{\frac {\theta ^{3}}{3!}}+{\frac {\theta ^{5}}{5!}}+\cdots \right)\\[8pt]&=\cos \theta +i\sin \theta ,\end{aligned}}$

where in the last step we recognize the two terms are the Maclaurin series for $cos\theta$ and $sin\theta$. The rearrangement of terms is justified because each series is absolutely convergent.

Εσωτερική Αρθρογραφία

• Απειροστή Στροφή
• μετασχηματισμός
• Μετασχηματισμός Γαλιλαίου
• Μετασχηματισμός Lorentz
• Απειροστικός Μετασχηματισμός
• απειροστό
• Ενιαία Μήτρα Απειροστής Στροφής

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• mathworld.wolfram.com
• webhome.phy.duke.edu

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---