Αρχιμήδης ο Συρακόσιος



Αρχιμήδης
μοχλός

Αρχή Αρχιμήδους
Άνωση
ανακάλυψη
εύρεση

Η τελευταία επιθυμία του Αρχιμήδη ήταν
να χαραχθεί στον τάφο του
η σφαίρα εγγεγραμμένη σε κύλινδρο
προς ανάμνηση του θεωρήματός του ότι
Vs/Vc = 2/3.
Το θεώρημα αυτό το απέδειξε
στο έργο του "Περί σφαίρας και κυλίνδρου".
Όταν ο Κικέρων, πολλά έτη μετέπειτα πήγε στις Συρακούσες,
και επισκέφθηκε το νεκροταφείο της πόλεως,
κοντά στην Ακραγαντίνη πύλη
ανακάλυψε τον τάφο του Αρχιμήδη
από το χαραγμένο σχήμα
της σφαίρας εγγεγραμμένης σε κύλινδρο.
Αρχή Αρχιμήδους
Άνωση
ανακάλυψη εύρεση
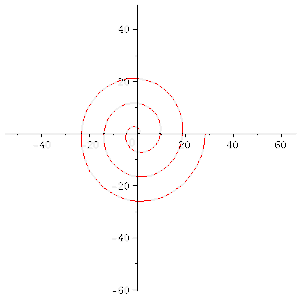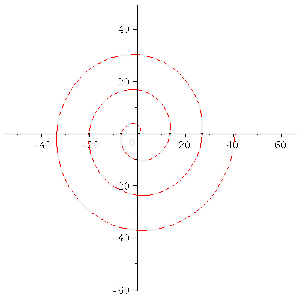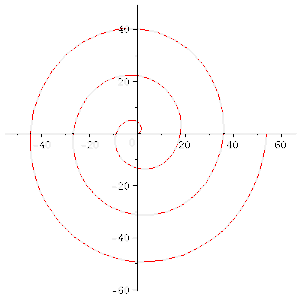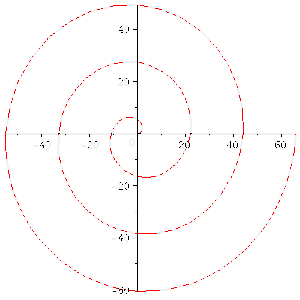

Αρχή Αρχιμήδους
Άνωση
ανακάλυψη &εύρεση

Επιστήμονες Αρχαίας Εποχής
Φυσικοί Αρχαίας Εποχής
Μαθηματικοί Αρχαίας Εποχής
Μηχανικοί Αρχαίας Εποχής

Αρχιμήδης

Αισχύλος

στα τείχη των Συρακουσών
καίει με κάτοπτρα τον Ρωμαϊκό Στόλο

Μαθηματικοί Αρχαίας Εποχής
Μαθηματικοί Γης
Μαθηματικοί Χιλιετιών Γης
Μαθηματικοί Εποχών Γης
Μαθηματικοί Αρχαϊκής Εποχής
Μαθηματικοί Κλασσικής Εποχής
Μαθηματικοί Ελληνιστικής Εποχής
Μαθηματικοί Ρωμαϊκής Εποχής
Μαθηματικοί Μεσαιωνικής Εποχής
Μαθηματικοί Νεώτερης Εποχής
Μαθηματικοί Σύγχρονης Εποχής
Γεωμετρία
Άλγεβρα
Τριγωνομετρία
Αριθμητική

Μηχανικοί Γης
Μηχανικοί Χιλιετιών Γης
Μηχανική
Μηχανολογία
Αρχαία Εποχή

Άνωση

θάνατος
- Ένας Σικελιώτης μαθηματικός και φυσικός.
- Χρονική Περίοδος Ακμής: Κλασσική Εποχή, 3ος Αιώνας π.Χ.
- Γέννηση: 287 π.Χ., Συρακούσες της Σικελίας.
- Θάνατος: 212 π.Χ.
Ετυμολογία[]
Το όνομα "Αρχιμήδης" συνδέεται ετυμολογικά με την λέξη "αρχή".
Γενεαλογία[]
- Πατέρας:
- Μητέρα:
- Σύζυγος:
- Τέκνα:
Βιογραφία[]
Τα σημαντικότερα βιογραφικά στοιχεία του είναι:
Ο Αρχιμήδης ο Συρακούσιος (ή Αρχιμήδης, περ. 287 π.Χ. – περ. 212 π.Χ.) ήταν αρχαίος Έλληνας μαθηματικός, μηχανικός, φυσικός, εφευρέτης και αστρονόμος.[1] Αν και λίγες λεπτομέρειες από τη ζωή του είναι γνωστές, θεωρείται ένας από τους κορυφαίους επιστήμονες στην κλασική αρχαιότητα. Η παρακαταθήκη του στη φυσική είναι, μεταξύ άλλων, οι βάσεις της υδροστατικής, της στατικής και μια εξήγηση της αρχής του μοχλού. Αυτός πιστώνεται με τον σχεδιασμό καινοτόμων μηχανών, συμπεριλαμβανομένων των πολιορκητικών μηχανών και των αντλιών με κοχλία που φέρουν το όνομά του. Αντικείμενο έρευνας έχουν αποτελέσει οι ισχυρισμοί πως ο Αρχιμήδης σχεδίασε μηχανές ικανές να επιτίθενται σε πλοία, να τα σηκώνουν έξω από το νερό και να τα πυρπολούν, χρησιμοποιώντας μια σειρά από καθρέφτες.[2]
Ο Αρχιμήδης θεωρείται ότι είναι ο σπουδαιότερος από τους μαθηματικούςτης αρχαιότητας και ένας από τους σπουδαιότερους όλων των εποχών.[3][4] Χρησιμοποίησε τη μέθοδο της εξάντλησης, για τον υπολογισμό της περιοχής, κάτω από το τόξο παραβολής, με την άθροιση άπειρης σειράς και έδωσε μια εξαιρετικά ακριβή προσέγγιση για τον αριθμό Π.[5] Όρισε, επίσης, την επίπεδη έλικα (σπείρα) που έφερε το όνομά του, φόρμουλες για τον όγκο των επιφανειών εκ περιστροφής και ένα ευφυές σύστημα για την έκφραση πολύ μεγάλων αριθμών.
Κατά την πολιορκία των Συρακουσών σκοτώθηκε από ένα Ρωμαίο στρατιώτη, παρά τις εντολές ότι δεν έπρεπε να τον πειράξουν. Ο Κικέρων επισκέφθηκε τον τάφο του Αρχιμήδη και αναφέρει πως επιστεφόταν από μια σφαίρα εγγεγραμμένη στο εσωτερικό ενός κυλίνδρου. Ο Αρχιμήδης είχε αποδείξει ότι η επιφάνεια κι ο όγκος μιας σφαίρας είναι τα 2/3 των αντίστοιχων του περιγεγραμμένου στη σφαίρα κλειστού κυλίνδρου και αυτό θεωρείται ως το μεγαλύτερο των μαθηματικών επιτευγμάτων του.
Αντίθετα με τις εφευρέσεις του, τα μαθηματικά κείμενα του Αρχιμήδη ήταν ελάχιστα γνωστά στην αρχαιότητα. Αν και μαθηματικοί από την Αλεξάνδρεια μελέτησαν και αναφέρθηκαν σε αυτόν, η πρώτη κατανοητή ολοκληρωμένη συλλογή δεν ήταν έτοιμη μέχρι περίπου το 530 μ.Χ., από τον Ισίδωρο τον Μιλήσιο, ενώ σχόλια επάνω στα έργα του Αρχιμήδη γράφτηκαν από τον Ευτόκιο και αυτά γνωστοποιήθηκαν στο ευρύτερο κοινό για πρώτη φορά τον έκτο αιώνα μ.Χ.. Τα σχετικά λιγοστά αντίγραφα των γραπτών εργασιών του Αρχιμήδη επιβίωσαν κατά τον Μεσαίωνα, και αποτέλεσαν μια πηγή επιρροής ιδεών για τους επιστήμονες κατά τη διάρκεια της Αναγέννησης.[6] Η ανακάλυψη το 1906 προηγούμενων άγνωστων εργασιών στο χειρόγραφο γνωστό ως Παλίμψηστο του Αρχιμήδη, παρείχε γνώσεις για το πως κατέληξε σε αυτά τα μαθηματικά του αποτελέσματα.[7]
Βιογραφία[]
Ο Αρχιμήδης γεννήθηκε περίπου το 287 π.Χ. στις Συρακούσες, στη Σικελία. Η ημερομηνία γέννησής του προέρχεται από μια πληροφορία του Βυζαντινού ιστορικού Ιωάννη Τζέτζη, που αναφέρει ότι ο Αρχιμήδης έζησε 75 έτη.[8]
Στον Ψαμμίτη, ο Αρχιμήδης αναφέρει ότι ο πατέρας του ονομαζόταν Φειδίας, ο οποίος ήταν ένας αστρονόμος για τον οποίο δεν υπάρχει τίποτα γνωστό.
Ο Πλούταρχος έγραψε στο έργο του "Βίοι Παράλληλοι" ότι ο Αρχιμήδης ήταν συγγενής και φίλος με τον βασιλέα Ιέρωνα Β', των Συρακουσών.[9]
Μια βιογραφία του Αρχιμήδη είχε γραφεί από τον φίλο του Ηρακλείδη, αλλά η εργασία του αυτή έχει χαθεί, αφήνοντας τις λεπτομέρειες της ζωής του στο σκότος.[10]
Είναι άγνωστο, αν ο Αρχιμήδης σπούδασε στην Αλεξάνδρεια της Αιγύπτου, όπου ο Κόνων ο Σάμιος και ο Ερατοσθένης ο Κυρηναίος ήταν σύγχρονοί του.
Αναφέρει τον Κόνωνα τον Σάμιο ως φίλο του, και δύο από τα ιστορικά έργα του (Η μέθοδος Μηχανολογικών Θεωρημάτων) και το Πρόβλημα των Βοοειδών έχουν εισαγωγές που απευθύνονται στον Ερατοσθένη.[a]
Ο Αρχιμήδης απέθανε περίπου το 212 π.Χ. κατά τη διάρκεια του 2ου Καρχηδονιακού Πολέμου, όταν οι Ρωμαϊκές δυνάμεις υπό τον στρατηγό Μάρκο Κλαύδιο Μάρκελλο κυρίευσαν την πόλη των Συρακουσών μετά από πολιορκία δύο ετών.
Σύμφωνα με τον Πλούταρχο, ο Αρχιμήδης είχε κατά νου ένα μαθηματικό διάγραμμα όταν η πόλη είχε καταληφθεί και δεν είχε αντιληφθεί την άλωσή της.
Ένας Ρωμαίος στρατιώτης τον διέταξε να μεταβεί και να συναντήσει τον στρατηγό Μάρκο Κλαύδιο Μάρκελλο αλλά αυτός αρνήθηκε λέγοντας ότι έπρεπε να τελειώσει το πρόβλημα του. Ο στρατιώτης εξοργίστηκε και σκότωσε τον Αρχιμήδη με το ξίφος του.
Άλλη εκδοχή που δίνει ο Πλούταρχος είναι ότι καθώς ο Ρωμαίος στρατιώτης ορμούσε με γυμνό ξίφος, ο Αρχιμήδης τον παρακάλεσε, μάταια όμως, να περιμένει λίγο ώστε να μή μείνει άλυτο το πρόβλημα που τον απασχολούσε.
Τρίτη τέλος εκδοχή του Πλουτάρχου είναι ότι ο Αρχιμήδης μεταβαίνοντας προς τον Μάρκελλο είχε μαζί του μαθηματικά όργανά, και τον σκότωσαν στρατιώτες επειδή νόμιζαν ότι ήταν πολύτιμα αντικείμενα.
Ο Μάρκελλος όταν πληροφορήθηκε τον θάνατο του Αρχιμήδη λυπήθηκε πολύ καθώς τον θεωρούσε ως ένα πολύτιμο κεφάλαιο για την επιστήμη και είχε διατάξει να μην θανατωθεί, εξοργίστηκε με τον στρατιώτη και ευεργέτησε τους οικείους του Αρχιμήδη.[11][12]
Οι τελευταίες λέξεις που του αποδίδονται είναι «μή μου τοὺς κύκλους τάραττε», αναφερόμενος στους κύκλους στο μαθηματικό του σχέδιο το οποίο υποτίθεται ότι μελετούσε όταν τον διέκοψε ο Ρωμαίος στρατιώτης. Συχνά αυτό τιμητικά αποδίδεται στα λατινικά ως «Noli turbare circulos meos», αλλά δεν υπάρχουν αξιόπιστα στοιχεία ότι ο Αρχιμήδης πρόφερε αυτές τις λέξεις και δεν εμφανίζονται στα γραπτά που μας έχουν διασωθεί από τον Πλούταρχο.[12]
Ο τάφος του Αρχιμήδη είχε ένα γλυπτό που απεικόνιζε την αγαπημένη μαθηματική απόδειξη του, αποτελούμενη από μία σφαίρα και ένα κύλινδρο με το ίδιο ύψος και διάμετρο. Ο Αρχιμήδης είχε αποδείξει ότι η επιφάνεια κι ο όγκος μιας σφαίρας είναι τα 2/3 των αντίστοιχων του κλειστού κυλίνδρου που την περιγράφει.
Το 75 π.Χ., 137 χρόνια μετά τον θάνατό του, ο Ρωμαίος ρήτορας Κικέρων υπηρετούσε ως κυαίστορας στη Σικελία. Είχε ακούσει ιστορίες για τον τάφο του Αρχιμήδη, αλλά κανένας από τους ντόπιους δεν ήταν σε θέση να προσδιορίσει τη θέση του τάφου. Ενδεχομένως βρήκε τον τάφο κοντά στην Ακραγαντινή πύλη των Συρακουσών, σε παραμελημένη κατάσταση και κατάφυτη από θάμνους. Ο Κικέρων διέταξε να καθαρίσουν τον τάφο, και ήταν σε θέση να δει το σκάλισμα και να διαβάσει μερικά από τα εδάφια, που είχαν προστεθεί ως επιγραφή.[13]
Ένα ελληνιστικό μαυσωλείο, που ανακαλύφθηκε στην αυλή ενός ξενοδοχείου που ανεγέρθη στις Συρακούσες στις αρχές του 1960, θεωρήθηκε από τον Ciancio ότι είναι ο τάφος του Αρχιμήδη.
Αλλά ο ανασκαφέας, ο έφορος αρχαιοτήτων Συρακουσών, Gentili, προτείνει την ταύτιση με ένα σημαντικό πρόσωπο της εποχής του Αγαθοκλέους (ίσως του ίδιου του βασιλέα).[14]
Οι βασικές εκδοχές της ζωής του Αρχιμήδη γράφηκαν πολύ καιρό μετά το θάνατό του από τους ιστορικούς της αρχαίας Ρώμης. Ο απολογισμός της πολιορκίας των Συρακουσών δίνεται από τον Πολύβιο στις Ιστορίες του που γράφηκαν εβδομήντα έτη μετά τον θάνατο του Αρχιμήδους, και χρησιμοποιήθηκαν στη συνέχεια ως πηγή από τον Πλούταρχο και τον Λίβιο. Αυτός έδωσε πληροφορίες για τον Αρχιμήδη ως πρόσωπο, και επικεντρώθηκε στις πολεμικές μηχανές που λέγεται ότι είχαν κατασκευασθεί για να υπερασπίσουν την πόλη.[15]
Ανακαλύψεις και εφευρέσεις[]
Η Αρχή του Αρχιμήδη[]
Η πιο γνωστή ιστορία για τον Αρχιμήδη αφορά την μέθοδο που εφηύρε για τον προσδιορισμό του όγκου ενός αντικειμένου με ακανόνιστο σχήμα. Σύμφωνα με τον Βιτρούβιο, ο βασιλέας Ιέρων Β είχε παραγγείλει την κατασκευή αναθηματικού στέμματος από ατόφιο χρυσό. Επειδή δεν είχε εμπιστοσύνη στον χρυσοχόο, ζήτησε από τον Αρχιμήδη να εξετάσει αν ο χρυσός είχε νοθευτεί με άργυρο.
Επειδή ο Αρχιμήδης έπρεπε να λύσει το πρόβλημα χωρίς να καταστρέψει το στέμμα, δεν μπορούσε να το τήξει προκειμένου να υπολογίσει την πυκνότητα του και την προέλευση του. Παρατήρησε ότι η στάθμη του ύδατος στην μπανιέρα ανέβηκε όταν εισήλθε ο ίδιος μέσα, και συνειδητοποίησε ότι αυτή η επίδραση θα μπορούσε να χρησιμοποιηθεί για τον προσδιορισμό του όγκου του στέμματος.
Με την παραδοχή ότι το ύδωρ πρακτικά είναι ασυμπίεστο, το αποτέλεσμα της βύθισης θα ήταν το στέμμα να εκτοπίσει μια ποσότητα ύδατος ίση με τον δικό του όγκο.
Διαιρώντας την μάζα του στέμματος με τον όγκο του ύδατος που εκτοπίζεται, προκύπτει η πυκνότητα του στέμματος. Αυτή η πυκνότητα θα είναι μικρότερη από εκείνη του χρυσού, εάν κάποια φθηνότερα και λιγότερο πυκνά μέταλλα είχαν προστεθεί. Ο Αρχιμήδης ενθουσιάστηκε τόσο από την ανακάλυψή του ώστε βγήκε στο δρόμο γυμνός φωνάζοντας «Εύρηκα|Εύρηκα! Εύρηκα!».
Η εξέταση του στέμματος απέδειξε νοθεία με σίδηρο.
Η ιστορία του χρυσού στέμματος δεν εμφανίζεται στα γνωστά έργα του Αρχιμήδη. Επιπλέον, η πρακτικότητα της μεθόδου που περιγράφει έχει αμφισβητηθεί, λόγω της υψηλής ακρίβειας που χρειάζεται κάποιος για να μετρήσει τη μετατόπιση νερού.
Αντ' αυτού ο Αρχιμήδης αναζήτησε μια λύση της υδροστατικής που αναφέρεται ως η γνωστή αρχή Αρχιμήδους, την οποία ο ίδιος περιγράφει στο σύγγραμμά του Περί επιπλέοντων σωμάτων.
Αυτή η αρχή δηλώνει ότι ένα σώμα που βυθίζεται σε ένα ρευστό δέχεται μια δύναμη άνωσης ίση με το βάρος του υγρού που εκτοπίζει.
Χρησιμοποιώντας αυτή την αρχή, θα ήταν δυνατή η σύγκριση της πυκνότητας της χρυσής στεφάνης με εκείνη του στερεού χρυσού με την εξισορρόπηση της κορώνας σε ένα ζυγό με ένα δείγμα αναφοράς χρυσού, και στη συνέχεια βυθίζοντας τη συσκευή στο νερό. Η διαφορά πυκνότητας μεταξύ των δύο δειγμάτων θα μπορούσε να προκαλέσει την κλίμακα να ανατραπεί αναλόγως.
Ο Γαλιλαίος έκρινε ότι «πιθανολογείται ότι η μέθοδος αυτή είναι η ίδια που ακολούθησε ο Αρχιμήδης, δεδομένου ότι, εκτός του ότι είναι πολύ ακριβής, βασίζεται σε επιδείξεις που παρουσίασε ο Αρχιμήδης ο ίδιος".
Σε ένα κείμενο του 12ου αιώνα με τίτλο Mappae clavicula υπάρχουν οδηγίες για το πώς να εκτελέσει κανείς τις ζυγίσεις στο νερό προκειμένου να υπολογίσει το ποσοστό του αργύρου που χρησιμοποιήθηκε, και ως εκ τούτου την επίλυση του προβλήματος. Το λατινικό ποίημα Carmen de ponderibus et mensuris του 4ου ή 5ου αιώνα περιγράφει τη χρήση της υδραυλικής ισορροπίας για την επίλυση του προβλήματος της κορώνας, και αποδίδει την μέθοδο στον Αρχιμήδη.
Κοχλίας του Αρχιμήδη[]
Πρότυπο:Κύριο
Ο κοχλίας του Αρχιμήδη μπορεί να ανεβάσει το νερό αποτελεσματικά.
Ένα μεγάλο μέρος του έργου του Αρχιμήδη στη μηχανική προέκυψε από την ικανοποίηση των αναγκών της γενέτειρας πόλης του, των Συρακουσών. Ο Αθήναιος αναφέρει πώς ο βασιλιάς Ιέρων Β΄ ανέθεσε στον Αρχιμήδη να σχεδιάσει ένα τεράστιο πλοίο, τη Συρακουσία, το οποίο θα μπορούσε να χρησιμοποιηθεί για ταξίδια αναψυχής, για μεταφορά προμηθειών και ως πολεμικό πλοίο.[16] Σύμφωνα με τον Αθήναιο, ήταν ικανό να μεταφέρει 600 άτομα και περιλάμβανε διακοσμητικούς κήπους, ένα γυμναστήριο και ένα ναό αφιερωμένο στη θεά Αφροδίτη. Δεδομένου ότι σε ένα πλοίο αυτού του μεγέθους θα διέρρεε σημαντική ποσότητα νερού διαμέσου του κύτους, ο κοχλίας του Αρχιμήδη εικάζεται ότι αναπτύχθηκε με σκοπό την απομάκρυνση του νερού. Ο μηχανισμός συνίστατο σε ένα περιστρεφόμενο κοχλία σε σχήμα λεπίδας μέσα σε έναν κύλινδρο. Γυρνούσε χειροκίνητα και μπορούσε επίσης να χρησιμοποιηθεί για τη μεταφορά νερού από ένα χαμηλού επίπεδου σώμα του νερού σε κανάλια άρδευσης. Ο κοχλίας του Αρχιμήδη είναι ακόμα σε χρήση σήμερα για την άντληση υγρών και στερεών σε κόκκους, όπως ο άνθρακας και το σιτάρι. Ο κοχλίας του Αρχιμήδη όπως περιγράφονταν στα ρωμαϊκά χρόνια από τον Βιτρούβιο μπορεί να ήταν μια βελτίωση σε σχέση με μία αντλία-κοχλία που είχε χρησιμοποιηθεί για την άρδευση των Κρεμαστών Κήπων της Βαβυλώνας.[17][18][19] Το πρώτο στον κόσμο ατμόπλοιο με βιδωτή έλικα ήταν το SS Archimedes, το οποία ξεκίνησε να λειτουργεί το 1839 και ονομάστηκε έτσι προς τιμήν του Αρχιμήδη και του έργου του πάνω στον κοχλία.[20]
Αρπάγη του Αρχιμήδη[]
Η αρπάγη του Αρχιμήδη είναι ένα όπλο που λέγεται ότι είχε σχεδιαστεί για την άμυνα των Συρακουσών. Επίσης γνωστή ως «αναδευτής πλοίων», η αρπάγη αποτελούνταν από ένα βραχίονα-γερανό, από τον οποίο αναπτύσσονταν ένας μεγάλος μεταλλικός γάντζος. Όταν η αρπάγη θα έπεφτε πάνω στο επιτιθέμενο πλοίο ο βραχίονας θα ταλαντευόταν προς τα πάνω, τραβώντας το πλοίο έξω από το νερό και προκαλώντας τη βύθισή του. Υπήρξαν σύγχρονα πειράματα για να ελεγχθεί η σκοπιμότητα της Αρπάγης και το 2005 ένα τηλεοπτικό ντοκιμαντέρ με τίτλο Υπερόπλα του Αρχαίου Κόσμου, κατασκεύασε μια έκδοση της Αρπάγης και κατέληξε στο συμπέρασμα ότι ήταν μια λειτουργική συσκευή.[21][22]
Έλιξ του Αρχιμήδους
Ακτίνα φωτός[]
Ο Αρχιμήδης μπορεί να χρησιμοποίησε καθρέπτες οι οποίοι λειτουργούσαν συγκεντρωτικά σαν παραβολικό κάτοπτρο και έκαιγαν τα πλοία που επιτίθονταν στις Συρακούσες.
Το 2ο αιώνα μ.Χ. ο συγγραφέας Λουκιανός έγραψε ότι κατά τη διάρκεια της Πολιορκίας των Συρακουσών (214-212 π.Χ.), ο Αρχιμήδης κατέστρεψε εχθρικά πλοία με τη χρήση της φωτιάς. Αιώνες αργότερα, ο Ανθέμιος ο Τραλλιανός αναφέρει το φλεγόμενο γυαλί ως το όπλο του Αρχιμήδη.[23] Η συσκευή, γνωστή και ως «Ακτίνα φωτός του Αρχιμήδη», χρησιμοποιούνταν για να συγκεντρώνει το ηλιακό φως στα επερχόμενα πλοία, με αποτέλεσμα αυτά να παίρνουν φωτιά.
Αυτό το υποτιθέμενο όπλο υπήρξε θέμα συνεχόμενης διαμάχης από την Αναγέννηση. Ο Ρενέ Ντεκάρτ το απέρριψε ως λανθασμένο, ενώ νέες έρευνες έχουν αποπειραθεί να αναπαραστήσουν το αποτέλεσμα χρησιμοποιώντας μόνο τα μέσα που ήταν διαθέσιμα στον Αρχιμήδη.[24] Έχει προταθεί ότι μια μεγάλη παράταξη από αρκετά γυαλισμένες μπρούτζινες ή χάλκινες ασπίδες οι οποίες λειτουργούσαν σαν καθρέπτες θα μπορούσαν να είχαν χρησιμοποιηθεί για να συγκεντρώσουν το ηλιακό φως στο πλοίο. Αυτό θα βασιζόταν στην αρχή του παραβολικού κατόπτρου με παρόμοιο τρόπο όπως σε έναν ηλιακό φούρνο.
Μια δοκιμή της ακτίνας φωτός του Αρχιμήδη έγινε το 1973 από τον Έλληνα επιστήμονα Ιωάννη Σάκκα. Το πείραμα έλαβε χώρα στη ναυτική βάση του Σκαραμαγκά έξω από την Αθήνα. Για αυτή τη περίπτωση χρησιμοποιήθηκαν 70 καθρέπτες, ο καθένας με χάλκινη επίστρωση και μέγεθος περίπου στα 1,5 επί 1 m. Οι καθρέπτες στράφηκαν σε ένα ομοίωμα από κόντρα πλακέ ενός Ρωμαϊκού πολεμικού πλοίου το οποίο βρισκόταν σε απόσταση κοντά στα 50 m. Όταν οι καθρέπτες σημάδεψαν με ακρίβεια το πλοίο, αυτό έπιασε φωτιά μέσα σε λίγα δευτερόλεπτα. Το πλοίο από κόντρα πλακέ ήταν επιστρωμένο με βαφή πίσσας, η οποία μπορεί να βοήθησε στην ανάφλεξη.[25] Η επίστρωση με βαφή πίσσας ήταν κοινότοπη στα πλοία την κλασσική εποχή.[d]
Τον Οκτώβριο του 2005 μια ομάδα φοιτητών του Τεχνολογικού Ινστιτούτου Μασαχουσέτης διεξήγαγε ένα πείραμα με 127 τετραγωνικά κεραμίδια καθρέπτη 30 cm, στοχεύοντας ένα ομοίωμα ξύλινου πλοίου σε απόσταση περίπου 30 m. Φλόγες ξέσπασαν σε ένα μπάλωμα του πλοίου αλλά μόνο όταν ο ουρανός δεν είχε σύννεφα και το πλοίο παρέμεινε στη θέση του για περίπου 10 λεπτά. Προέκυψε το συμπέρασμα ότι η παράταξη ήταν ένα εφικτό όπλο κάτω από αυτές τις συνθήκες. Η ομάδα του ΜΙΤ επανέλαβε το πείραμα για την τηλεοπτική εκπομπή MythBusters, χρησιμοποιώντας μια ξύλινη βάρκα ψαρέματος στο Σαν Φρανσίσκο ως στόχο. Ξανά συνέβη μερική απανθράκωση, μαζί με μια μικρή φωτιά. Για να πιάσει φωτιά, το ξύλο χρειάζεται να φτάσει στη θερμοκρασία αυτανάφλεξης, που είναι γύρω στους 300 °C.[26][27]
Όταν οι Mythbusters πρόβαλαν το αποτέλεσμα του πειράματος στο Σαν Φρανσίσκο τον Ιανουάριο του 2006, ο μύθος τοποθετήθηκε στην κατηγορία των «κατερριμένων» λόγω του χρόνου και των ιδανικών καιρικών συνθηκών που χρειαζόταν για να συμβεί η ανάφλεξη. Επίσης τονίστηκε ότι αφού οι Συρακούσες έβλεπαν την θάλασσα προς τα ανατολικά, ο ρωμαϊκός στόλος θα έπρεπε να επιτεθεί κατά τη διάρκεια του πρωινού για βέλτιστη συγκέντρωση φωτός από τους καθρέπτες. Οι Mythbusters τόνισαν επίσης ότι συμβατικά όπλα όπως φλεγόμενα βέλη ή βίδες από τους καταπέλτες θα ήταν ένας πολύ εύκολος τρόπος για να βάλουν φωτιά σε ένα πλοίο σε κοντινές αποστάσεις.[2]
Τον Δεκέμβριο του 2010, οι Mythbusters άνοιξαν ξανά την υπόθεση της ακτίνας φωτός σε ένα σπέσιαλ επεισόδιο όπου συμμετείχε και ο Μπαράκ Ομπάμα με τον τίτλο «Η Πρόκληση του Προέδρου». Αρκετά πειράματα διεξήχθησαν, συμπεριλαμβανομένης και μιας δοκιμής μεγάλης κλίμακας με 500 μαθητές να σημαδεύουν με τους καθρέπτες ένα ομοίωμα ενός ρωμαϊκού πλοίου σε απόσταση 120 m. Σε όλα τα πειράματα το ιστίο απέτυχε να φτάσει στους 210 °C που απαιτούνται για να πιάσει φωτιά και ο μύθος τοποθετήθηκε εκ νέου στην κατηγορία των «κατερριμένων». Η εκπομπή συμπέρανε πως ένα πιο πιθανό αποτέλεσμα των καθρεφτών θα ήταν να τυφλώνει, να εκθαμβώνει και να αποσπά την προσοχή του πληρώματος του πλοίου.[28]
Άλλες ανακαλύψεις και εφευρέσεις[]
Παρότι δεν ήταν ο Αρχιμήδης που εφηύρε τον μοχλό, έδωσε μια εξήγηση για την αρχή στην οποία βασίζεται η χρήση του στο έργο του Περί επιπέδων ισορροπιών. Αρχαιότερες περιγραφές του μοχλού μπορούν να βρεθούν στην Περιπατητική Σχολή των υποστηρικτών του Αριστοτέλη και μερικές φορές αυτές αποδίδονται στον Αρχύτα.[29][30] Σύμφωνα με τον Πάππο τον Αλεξανδρέα, το έργο του Αρχιμήδη πάνω στους μοχλούς τον έκανε να παρατηρήσει: «Δώστε μου ένα σημείο να στηριχθώ και θα κινήσω τη Γη» (αρχαία: δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω).[31] O Πλούταρχος περιγράφει πώς ο Αρχιμήδης σχεδίαζε ανυψωτικά συστήματα τροχαλιών επιτρέποντας στους ναυτικούς να χρησιμοποιούν την αρχή της μόχλευσης για να σηκώνουν αντικείμενα που ειδάλλως δεν θα μπορούσαν να σηκώσουν.[32][33] Στον Αρχιμήδη επίσης αποδίδεται η βελτίωση της δύναμης και της ακρίβειας του καταπέλτη καθώς και η εφεύρεση του οδομετρητή κατά τη διάρκεια του πρώτου Καρχηδονιακού πολέμου. Ο οδομετρητής περιγράφεται ως ένα κάρο με μηχανισμό γραναζιού που έριχνε μια μπάλα σε ένα κιβώτιο κάθε φορά που συμπλήρωνε ένα μίλι.[34] Επίσης κατασκεύασε ένα υδραυλικό ρολόι το οποίο υπολόγιζε με μεγάλη ακρίβεια τις ώρες και ειδοποιούσε για την αλλαγή της ώρας.
Ο Κικέρων(106-43 π.Χ.) αναφέρει εν συντομία τον Αρχιμήδη στο διάλογό του Περί δημοκρατίας, που απεικονίζει μια φανταστική συζήτηση η οποία λαμβάνει χώρα το 129 π.Χ.. Μετά την κατάκτηση των Συρακουσών το 212 π.Χ. λέγεται ότι ο Στρατηγός Μάρκος Κλαύδιος Μάρκελλος πήρε πίσω στη Ρώμη δύο μηχανισμούς, που κατασκευάσθηκαν από τον Αρχιμήδη και με εφαρμογή στην αστρονομία, το οποίο έδειχνε την κίνηση του Ηλίου, της Σελήνης και πέντε πλανητών. Ο Κικέρων αναφέρει παρόμοιους μηχανισμούς σχεδιασμένους από τον Θαλή τον Μιλήσιο και τον Εύδοξο τον Κνίδιο. Ο διάλογος λέει πως ο Μάρκελλος κράτησε τον ένα από τους μηχανισμούς ως το μοναδικό προσωπικό λάφυρο από τις Συρακούσες και δώρισε τον άλλο στο Ναό της Αρετής στη Ρώμη. Ο μηχανισμός του Μάρκελλου παρουσιάστηκε από τον Γάιο Σουλπίκιο Γάλλο στον Λούκιο Φούριο Φίλο ο οποίος τον περιέγραψε:
- Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione. —Όταν ο Γάλλος μετακίνησε την υδρόγειο, τότε η Σελήνη ακολούθησε τον Ήλιο σε όσες στροφές και αν έκανε σε αυτή τη μπρούντζινη συσκευή όπως θα γινόταν και στον ουρανό, από την οποία είδαμε ότι επίσης στον ουρανό η έκλειψη Ηλίου ήταν η ίδια όταν η Σελήνη ερχόταν σε εκείνη την θέση ώστε να ρίχνει την σκιά της πάνω στην Γη, όταν τα τρία σώματα ήταν ευθυγραμμισμένα.[35][36]
Αυτή είναι η περιγραφή ενός πλανητάριου ή πλανητοσκοπίου. Ο Πάππος ο Αλεξανδρεύς δήλωσε ότι ο Αρχιμήδης είχε γράψει ένα χειρόγραφο (σήμερα χαμένο) πάνω στην κατασκευή τέτοιων μηχανισμών με το τίτλο Περί σφαιροποιΐας. Πρόσφατες έρευνες σε αυτό το θέμα εστιάζουν στον Μηχανισμό των Αντικυθήρων, άλλη μία συσκευή από την κλασσική αρχαιότητα που πιθανότατα σχεδιάστηκε για τον ίδιο λόγο. Η δημιουργία τέτοιου είδους μηχανισμών θα απαιτούσε προχωρημένη γνώση για τη λειτουργία του διαφορικού. Αυτό πιστευόταν ότι ήταν πέρα των δυνατοτήτων της τεχνολογίας στις αρχαίες εποχές, αλλά η ανακάλυψη του Μηχανισμού των Αντικυθήρων το 1902 επιβεβαίωσε το γεγονός ότι συσκευές τέτοιου είδους ήταν γνωστές στους αρχαίους Έλληνες.[37][38]
Μαθηματικά[]
Ενώ συχνά θεωρείται ως σχεδιαστής μηχανικών συσκευών, ο Αρχιμήδης έκανε επίσης συνεισφορές στον τομέα των μαθηματικών. Ο Πλούταρχος έγραψε: «Αφιέρωσε όλη του τη στοργή και τη φιλοδοξία του σε αυτές τις καθαρότερες εικασίες όπου δεν μπορεί να γίνει αναφορά στις χυδαίες ανάγκες της ζωής.»[39]
Ο Αρχιμήδης χρησιμοποίησε το Πυθαγόρειο θεώρημα για να υπολογίσει την πλευρά του 12-γωνου από αυτή του εξαγώνου και για κάθε επακόλουθο διπλασιασμό των πλευρών του κανονικού πολυγώνου.
Ο Αρχιμήδης μπορούσε να χρησιμοποιήσει τα απειροελάχιστα με τρόπο παρόμοιο με τον Ολοκληρωτικό Λογισμό. Μέσω της Εις άτοπον απαγωγή απόδειξη μπορούσε να δώσει απαντήσεις σε προβλήματα έως ένα αυθαίρετο βαθμό ακρίβειας, προσδιορίζοντας τα όρια μέσα στα οποία ίσχυε η απάντηση. Αυτή η μέθοδος είναι γνωστή ως η Μέθοδος της εξάντλησης και την εφάρμοσε για να προσεγγίσει την τιμή του αριθμού π. Στο Κύκλου Μέτρησις το έκανε αυτό ζωγραφίζοντας ένα μεγαλύτερο κανονικό εξάγωνο έξω από τον κύκλο και ένα μικρότερο κανονικό εξάγωνο μέσα στο κύκλο και προοδευτικά διπλασιάζοντας τον αριθμό των πλευρών και στα δύο κανονικά πολύγωνα, υπολογίζοντας το μήκος της πλευράς κάθε πολυγώνου σε κάθε βήμα. Καθώς ο αριθμός των πλευρών αυξάνεται, γίνεται μια πιο ακριβής προσέγγιση του κύκλου. Μετά από 4 τέτοια βήματα, όταν τα πολύγωνα είχαν από 96 πλευρές το καθένα, ήταν σε θέση να προσδιορίσει ότι η τιμή του π βρισκόταν ανάμεσα στο 3Πρότυπο:Frac(περίπου 3,1429) και 3Πρότυπο:Frac(περίπου 3,1408) εντός των ορίων αφού η τιμή προσεγγιστικά είναι 3,1416.[40] Επίσης απέδειξε ότι το Εμβαδόν ενός κύκλου ισούται με το π πολλαπλασιασμένο με το τετράγωνο της ακτίνας του κύκλου (πr2). Στο Περί σφαίρας και κυλίνδρου δηλώνει ότι ένα μέγεθος όταν προστεθεί αρκετές φορές στον εαυτό του θα ξεπεράσει οποιοδήποτε άλλο μέγεθος. Αυτή είναι η Αρχιμήδεια ιδιότητα των πραγματικών αριθμών.[41]
Στο Κύκλου Μέτρησις ο Αρχιμήδης υποστηρίζει ότι η τετραγωνική ρίζα του 3 βρίσκεται ανάμεσα στο Πρότυπο:Frac (περίπου 1,7320261) και στο Πρότυπο:Frac (περίπου 1,7320512). Η πραγματική τιμή είναι περίπου 1,7320508, γεγονός που κάνει αυτό τον υπολογισμό πολύ ακριβή. Παρουσίασε αυτό το αποτέλεσμα χωρίς να προσφέρει καμία εξήγηση για το πως έφτασε σε αυτό. Αυτή η όψη του έργου του Αρχιμήδη ανάγκασε τον John Wallis να δηλώσει: «πιθανόν να κάλυψε τα ίχνη της ερευνάς του σκόπιμα επειδή θα ένιωθε ότι δίνει στους μεταγενέστερους το μυστικό της συλλογής πληροφοριών του, ενώ ταυτόχρονα ήθελε να αποσπάσει από αυτούς απαντήσεις για τα δικά του ευρήματα».[42] Είναι πιθανό να χρησιμοποιούσε επαναληπτικές διαδικασίες για να υπολογίσει αυτές τις τιμές.[43]
Όπως αποδείχθηκε από τον Αρχιμήδη το εμβαδόν του παραβολικού τμήματος στην πάνω εικόνα είναι ίσο με τα 4/3 του εμβαδού του εγγεγραμένου τριγώνου στην κάτω εικόνα.
Στο Τετραγωνισμός της παραβολής ο Αρχιμήδης απέδειξε ότι το εμβαδόν που περικλείεται από μία παραβολή και μια ευθεία γραμμή είναι Πρότυπο:Frac φορές το εμβαδόν του αντίστοιχου εγγεγραμμένου τριγώνου όπως φαίνεται στην εικόνα δεξιά. Εξέφρασε τη λύση στο πρόβλημα ως μία άπειρη Γεωμετρική σειρά με λόγο Πρότυπο:Frac.
Αν ο πρώτος όρος σε αυτή τη σειρά είναι το εμβαδόν του τριγώνου, τότε ο δεύτερος είναι το άθροισμα των εμβαδών των δύο τριγώνων των οποίων οι βάσεις είναι οι δύο μικρότερες διατέμνουσες γραμμές και ούτω καθεξής. Αυτή η απόδειξη χρησιμοποιεί μια παραλλαγή της σειράς 1/4 + 1/16 + 1/64 + 1/256 +... η οποία έχει άθροισμα το Πρότυπο:Frac.
Στο Ψαμμίτης, ξεκινά να υπολογίζει τον αριθμό των κόκκων άμμου που υπάρχουν στο σύμπαν. Στη προσπάθεια του, αντιτάχθηκε στην ιδέα ότι ο αριθμός των κόκκων άμμου ήταν πολύ μεγάλος για να υπολογισθεί. Έγραψε: «Υπάρχουν μερικοί, βασιλιά Γέλωνα (Γέλων ο Β΄, γιος του Ιέρωνα Β΄) που πιστεύουν ότι ο αριθμός της άμμου είναι άπειρος σε μέγεθος και όταν λέω άμμου δεν εννοώ την άμμο που υπάρχει στις Συρακούσες και στην υπόλοιπη Σικελία αλλά και αυτή που βρίσκεται σε κάθε περιοχή είτε κατοικείται είτε όχι». Για να λύσει το πρόβλημα, ο Αρχιμήδης επινόησε ένα σύστημα μέτρησης με μονάδα μέτρησης την μυριάδα. Η λέξη προέρχεται από τη λέξη μυριάς, για τον αριθμό 10.000. Πρότεινε ένα σύστημα αρίθμησης χρησιμοποιώντας μυριάδα μυριάδων (100 εκατομμύρια) και συμπέρανε ότι ο αριθμός των κόκκων άμμου που χωράει το σύμπαν είναι 8 εικοσάκις εκατομμύρια ή 8Πρότυπο:E.[44]
Συγγράμματα[]
Τα έργα του Αρχιμήδη είχαν γραφεί στη δωρική διάλεκτο, τη διάλεκτο των Συρακουσών.[45] Τα γραπτά έργα του δεν έχουν διασωθεί όπως αυτά του Ευκλείδη, και επτά από τις πραγματείες του είναι γνωστό ότι υπήρχαν μόνο μέσα από αναφορές που γίνονται σε αυτές από άλλους συγγραφείς. Ο Πάππος ο Αλεξανδρεύς αναφέρει το έργο του Αρχιμήδη Περί σφαιροποιΐας καθώς κι ένα άλλο πάνω στα πολύεδρα, ενώ ο Θέων ο Αλεξανδρεύς κάνει μία παρατήρηση σχετικά με τη διάθλαση από το μη διασωθέν σήμερα έργο του Αρχιμήδη Κάτοπτρα.[b] Κατά τη διάρκεια της ζωής του, ο Αρχιμήδης έκανε το έργο του γνωστό μέσω αλληλογραφίας με τους μαθηματικούς στην Αλεξάνδρεια. Τα γραπτά του Αρχιμήδη συλλέχθηκαν από έναν αρχιτέκτονα της Βυζαντινής Αυτοκρατορίας ονόματι Ισίδωρος ο Μιλήσιος (περ. 530 μ.Χ.), ενώ τα σχόλια για τα έργα του Αρχιμήδη γραμμένα από τον Ευτόχιο στον έκτο μ.Χ. αιώνα, βοήθησαν να διαδοθεί το έργο του σε ένα ευρύτερο κοινό. Έργο του Αρχιμήδη μεταφράστηκε στα αραβικά από τον Ταμπίτ ιμπν Κουρά (836-901 μ.Χ.), και στη λατινική[46] από τον Γεράρδο της Κρεμόνα (περ. 1114-1187 μ.Χ.). Κατά τη διάρκεια της Αναγέννησης, η Editio Princeps (Πρώτη έκδοση), δημοσιεύθηκε στη Βασιλεία το 1544 από τον Johann Herwagen, με τα έργα του Αρχιμήδη στην ελληνική και λατινική. Το έτος 1586, ο Γαλιλαίος Γαλιλέι εφηύρε ένα υδροστατικό ζυγό για τη ζύγιση των μετάλλων στον αέρα και στο νερό, εμπνευσμένος προφανώς από το έργο του Αρχιμήδη.[47]
Διασωθέντα συγγράμματα[]
- Περί επιπέδων ισορροπιών ή κέντρα βαρών επιπέδων ή Μηχανικά, Βιβλ α' και β'
- Το πρώτο βιβλίο αποτελείται από δεκαπέντε προτάσεις και επτά αξιώματα, ενώ το δεύτερο βιβλίο περιέχει δέκα προτάσεις. Σε αυτό το έργο του ο Αρχιμήδης εξηγεί το Νόμο του Μοχλού δηλώνοντας ότι:
- "Τα μεγέθη είναι σε ισορροπία, όταν βρίσκονται σε αποστάσεις αντιστρόφως ανάλογες με το βάρος τους."
- Ο Αρχιμήδης χρησιμοποιεί τις αρχές που προκύπτουν, για τον υπολογισμό των εμβαδών και των κέντρων βάρους των διαφόρων γεωμετρικών σχημάτων, όπως τρίγωνα, παραλληλόγραμμα και παραβολές.[48]
- Κύκλου μέτρησις. Σώζονται τρία θεωρήματα.
- Αυτή είναι μια σύντομη εργασία που αποτελείται από τρεις προτάσεις. Είναι γραμμένη σε μορφή αλληλογραφίας με τον Δοσίθεο του Πηλουσίου, ο οποίος ήταν μαθητής του Κόνωνα του Σάμιου. Στη δεύτερη πρόταση, ο Αρχιμήδης δίνει μια προσέγγιση της τιμής του π, η οποία δείχνει ότι είναι μεγαλύτερη από Πρότυπο:Frac και μικρότερη από Πρότυπο:Frac.
- Περί ελίκων (28 προτάσεις, 6 πορίσματα)
- Αυτό το έργο των 28 προτάσεων, επίσης απευθυνόταν στον Δοσίθεο. Τούτη η πραγματεία ορίζει αυτό που σήμερα καλείται η σπείρα του Αρχιμήδη. Είναι ο γεωμετρικός τόπος των σημείων που αντιστοιχούν στο σύνολο των διάφορων θέσεων, από τις οποίες διέρχεται ένα σημείο, με την πάροδο του χρόνου, καθώς αυτό κινείται μακριά από ένα σταθερό σημείο με μια σταθερή ταχύτητα κατά μήκος μίας γραμμής, η οποία περιστρέφεται με σταθερή γΓωνιακή Ταχύτητα. Ισοδύναμα, σε πολικές συντεταγμένες (r, θ) μπορεί να περιγραφεί από την εξίσωση
- με πραγματικούς αριθμούς a και b. Αυτό είναι ένα πρώιμο παράδειγμα μιας μηχανικής καμπύλης (καμπύλη που διαγράφεται από ένα κινούμενο σημείο), που θεωρείται από Έλληνα μαθηματικό.
- Περί σφαίρας και κυλίνδρου, Βιβλίο α' και β'
- Στην πραγματεία αυτή απευθυνόμενος στον Δοσίθεο, ο Αρχιμήδης κατορθώνει κάτι το οποίο τον έκανε να είναι ιδιαίτερα περήφανος. Αυτό το κάτι ήταν η ανακάλυψη της σχέσης μεταξύ μίας σφαίρας κι ενός περιγεγραμμένου κυλίνδρου του ίδιου ύψους και της ίδιας διαμέτρου. Ο όγκος είναι Πρότυπο:Fracπr3 για τη σφαίρα, και 2πr3 για τον κύλινδρο. Το εμβαδόν επιφανείας είναι 4πr2 για τη σφαίρα, και 6πr2 για τον κύλινδρο (συμπεριλαμβανομένων των δύο βάσεων του), όπου r είναι η ακτίνα της σφαίρας και του κυλίνδρου. Η σφαίρα έχει όγκο τα δύο τρίτα του περιγεγραμμένου κυλίνδρου. Ομοίως, η σφαίρα έχει εμβαδόν τα δύο τρίτα του κυλίνδρου (συμπεριλαμβανομένων των βάσεων). Στον τάφο του Αρχιμήδη κατόπιν επιθυμίας του είχαν τοποθετηθεί δύο γλυπτά, μία σφαίρα κι ένας κύλινδρος.
- Περί κωνοειδέων και σφαιροειδέων (32 προτάσεις, 1 πόρισμα)
- Αυτό είναι ένα έργο αποτελούμενο από 32 προτάσεις, που απευθύνονται στον Δοσίθεο. Σε αυτή την πραγματεία του ο Αρχιμήδης υπολογίζει τα εμβαδά και τους όγκους τμημάτων από κώνους, σφαίρες και παραβολοειδή.
- Πρόβλημα βοοειδών του Αρχιμήδη (Πρόβλημα Βοεικόν)
- Το έργο ανακαλύφθηκε από τον Gotthold Ephraim Lessing σε ένα ελληνικό χειρόγραφο αποτελούμενο από ένα ποίημα από 44 γραμμές, στη βιβλιοθήκη Herzog August στο Wolfenbüttel της Γερμανίας, το 1773. Απευθύνεται στον Ερατοσθένη και στους μαθηματικούς στην Αλεξάνδρεια. Ο Αρχιμήδης τους προκαλεί να μετρήσουν τον αριθμό των βοοειδών στην Αγέλη του Ήλιου, με την ταυτόχρονη επίλυση ενός αριθμού Διοφαντικών εξισώσεων. Υπάρχει και μια πιο δύσκολη έκδοση του προβλήματος στην οποία μερικές από τις λύσεις απαιτείται να είναι τέλεια τετράγωνα. Αυτή η έκδοση του προβλήματος λύθηκε για πρώτη φορά από τον Α. Amthor[49] το 1880 και η απάντηση είναι ένας πολύ μεγάλος αριθμός, περίπου 7,760271Πρότυπο:E
- Ψαμμίτης
- Σε αυτή την πραγματεία του, ο Αρχιμήδης μετρά τον αριθμό των κόκκων της άμμου που μπορούν να χωρέσουν μέσα στο σύμπαν. Το βιβλίο αναφέρει την ηλιοκεντρική θεωρία του ηλιακού συστήματος που προτείνεται από τον Αρίσταρχο το Σάμιο, καθώς και σύγχρονες ιδέες σχετικά με το μέγεθος της Γης και την απόσταση μεταξύ διάφορων ουράνιων σωμάτων. Με τη χρήση ενός συστήματος αριθμών υψωμένων σε μυριάδες(μυριάδα=10.000), ο Αρχιμήδης καταλήγει πως ο αριθμός των κόκκων της άμμου που απαιτείται για να γεμίσει το σύμπαν είναι 8 x 1063 σε σύγχρονη σημειογραφία. Η εισαγωγική επιστολή αναφέρει ότι ο πατέρας του Αρχιμήδη ήταν αστρονόμος ονόματι Φειδίας. Ο Ψαμμίτης είναι το μόνο σωζόμενο έργο στο οποίο ο Αρχιμήδης συζητά τις απόψεις του σχετικά με την αστρονομία.[50]
- Τετραγωνισμός παραβολής
- Στο έργο αυτό που αποτελείται από 24 προτάσεις ο Αρχιμήδης απευθυνόμενος στο Δοσίθεο, αποδεικνύει με δύο μεθόδους ότι το εμβαδόν που περικλείεται από μια παραβολή και μια ευθεία γραμμή ισούται με πολλαπλασιαζόμενο επί το εμβαδό ενός τριγώνου με την ίδια βάση και ύψος. Αυτό το κατάφερε με τον υπολογισμό της αξίας της γεωμετρικής σειράς που αθροίζεται στο άπειρο με λόγο Πρότυπο:Frac.
Πρόσφατα (2006) διαβάστηκαν από το Παλίμψηστο του Αρχιμήδη αποσπάσματα από τα έργα που διασώθηκαν σε αυτό:
- Οστομάχιον
- Αυτό είναι ένα τεμαχισμένο παζλ παρόμοιο με ένα tangram, κι η πραγματεία που το περιέγραφε βρέθηκε σε πιο ολοκληρωμένη μορφή στο Παλίμψηστο του Αρχιμήδη. Ο Αρχιμήδης υπολογίζει τα εμβαδά των δεκατεσσάρων κομματιών, τα οποία συναρμολογούμενα μπορούν να σχηματίσουν ένα τετράγωνο. Έρευνα που δημοσιεύθηκε το 2003 από τον Δρ.Reviel Netz του Πανεπιστημίου του Στάνφορντ, υποστήριζε ότι ο Αρχιμήδης προσπαθούσε να καθορίσει με πόσους δυνατούς τρόπους θα μπορούσαν να τοποθετηθούν τα κομμάτια έτσι ώστε να συναρμολογήσουν ένα τετράγωνο. Ο Δρ Netz υπολογίζει πως τα κομμάτια μπορούν να δημιουργήσουν ένα τετράγωνο με 17.152 διαφορετικούς τρόπους.[51] Ο αριθμός των διατάξεων είναι 536, όταν οι λύσεις που είναι ισοδύναμες με περιστροφή κι αντανάκλαση έχουν αποκλειστεί.[52] Το παζλ αντιπροσωπεύει ένα παράδειγμα πρώιμου προβλήματος στη Συνδυαστική.
- Η προέλευση του ονόματος του παζλ είναι ασαφής, και έχει υποστηριχθεί ότι αυτό έχει ληφθεί από την αρχαία ελληνική λέξη για το λαιμό ή τον οισοφάγο, στόμαχος.[53] Ο Αυσόνιος αναφέρεται στο παζλ, με την ονομασία "Οστομάχιον", μια ελληνική σύνθετη λέξη που σχηματίζεται από τις ρίζες του ὀστέον (οστό) και της μάχης (αγώνας). Το παζλ είναι επίσης γνωστό ως μικρό πακέτο (loculus) του Αρχιμήδη ή Κουτί του Αρχιμήδη.[54]
- Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος (=μέθοδος)
- Η πραγματεία αυτή θεωρούνταν χαμένη μέχρι και την ανακάλυψη του Παλίμψηστου του Αρχιμήδη το 1906. Σε αυτό το έργο του, o Αρχιμήδης χρησιμοποιεί απειροστικά και δείχνει ότι η διαμέλιση ενός σχήματος σε έναν άπειρο αριθμό, απείρως μικρών τμημάτων, μπορεί να μας βοηθήσει στο να προσδιορίσουμε το εμβαδόν ή και τον όγκο του. Ο Αρχιμήδης είχε υπόψη του πως αυτή η μέθοδος στερείται επίσημης αυστηρότητας, έτσι χρησιμοποίησε και τη μέθοδο της εξάντλησης για την εξαγωγή των αποτελεσμάτων. Όπως και το Πρόβλημα Βοοειδών, έτσι κι αυτό το έργο ήταν γραμμένο με τη μορφή επιστολής προς τον Ερατοσθένη, στην Αλεξάνδρεια.
- Περί των επιπλεόντων σωμάτων
- Στο πρώτο μέρος αυτής της πραγματείας, ο Αρχιμήδης εξηγεί το νόμο της ισορροπίας των υγρών και αποδεικνύει ότι το ύδωρ θα υιοθετήσει μια σφαιρική μορφή γύρω από ένα κέντρο βαρύτητας. Αυτό μπορεί να ήταν μια προσπάθεια για να εξηγήσει τη θεωρία των τότε σύγχρονων Ελλήνων αστρονόμων, όπως και του Ερατοσθένη του Κυρηναίου, ότι η Γη είναι σφαιρική. Τα υγρά περιγράφονται από τον Αρχιμήδη ως μη αυτο-βαρυτικά, δεδομένου ότι υποθέτει την ύπαρξη ενός σημείου, προς το οποίο εμπίπτουν όλα τα αντικείμενα, με αποτέλεσμα να αποκτούν το σφαιρικό τους σχήμα.
- Στο δεύτερο μέρος, υπολογίζει τις θέσεις ισορροπίας διάφορων τμημάτων από παραβολοειδή. Αυτό ήταν ίσως μια εξιδανίκευση των σχημάτων, που δημιουργούσε το βυθισμένο μέρος των πλοίων στο νερό. Κάποια από αυτά τα τμήματα επιπλέουν με τη βάση κάτω από το νερό και τη μέγιστη (σε ύψος) κορυφή πάνω από το νερό, παρόμοια με τον τρόπο με τον οποίο τα παγόβουνα επιπλέουν. Η αρχή της άνωσης του Αρχιμήδη παρατίθεται σε αυτό το έργο, ως εξής:
- «Κάθε σώμα που είναι εξ ολοκλήρου ή μερικώς βυθισμένο σε ένα ρευστό, δέχεται μια ώθηση ίση σε μέγεθος, αλλά αντίθετης φοράς, με το βάρος του εκτοπισμένου ρευστού.»
- Κατασκευή πλευράς του περιγραφομένου εις κύκλο επταγώνου
- Ωρολόγιον Αρχιμήδους (Σώζεται στα αραβικά)
- Περί κύκλων εφαπτομένων αλλήλων
- Αρχαί της Γεωμετρίας
- Οχουμένων (Υδροστατική επιπλεόντων σωμάτων)
Απόκρυφα έργα[]
- Βιβλίο λημμάτων
- Το έργο του Αρχιμήδη Βιβλίο λημμάτων ή Liber Assumptorum είναι μια πραγματεία με δεκαπέντε προτάσεις σχετικά με τη φύση των κύκλων. Το αρχαιότερο γνωστό αντίγραφο του κειμένου είναι στα αραβικά. Οι μελετητές T. L. Heath και Marshall Clagett υποστήριζαν πως δεν μπορεί να έχει γραφεί από τον Αρχιμήδη, αυτό το έργο στη σημερινή του μορφή, δεδομένου ότι αναφέρει τον Αρχιμήδη σε τρίτο πρόσωπο, γεγονός που υποδηλώνει επεξεργασία από κάποιον άλλο συντάκτη. Το έργο αυτό μπορεί να βασίζεται σε μια προηγούμενη εργασία του Αρχιμήδη, η οποία πιθανότατα έχει χαθεί.[55]
- Επίσης, θεωρείται πως ο τύπος Ήρωνα για τον υπολογισμό του εμβαδού ενός τριγώνου από το μήκος των πλευρών του, ήταν γνωστός στον Αρχιμήδη. [56]O'Connor, J.J. and Robertson, E.F. (April 1999). Heron of Alexandria. University of St Andrews. http://www-history.mcs.st-and.ac.uk/Biographies/Heron.html. Ανακτήθηκε την 2010-02-17.</ref>
Μη διασωθέντα συγγράμματα[]
(ή συγγράμματα μη αποκαλυφθέντα μέχρι σήμερα)
- Αριθμητικά
- Βαρουλκός, Υδροσκοπίαι, Πνευματική
- Επισίδια Βιβλία (Μάλλον περί στατιστικής - Τζέτζης)
- Περί τριγώνων
- Περί τετραπλεύρου
- Περί ζευγών
- Περί 13 ημικανονικών πολυέδρων
- Ισοπεριμετικά
- Ισορροπίαι
- Καύσις δια κατόπτρων (επ΄ αυτού έγινε επιτυχές πείραμα στο Ν.Σ.)
- Περί Αρχιτεκτονικής
- Περί βαρύτητος και ελαφρότητος (Πυκνόμετρα - Αραιόμετρα)
- Περί δρομομέτρων (Οδόμετρα πλοίων)
- Περί κέντρου Βάρους ή Κεντροβαρικά
- Κατοπρικά
- Περί παραλλήλων γραμμών
- Περί κοίλων και παραβολικών κατόπτρων
- Προοπτική
- Στοιχεία μηχανικών
- Πλινθίδες και Κύλινδροι
- Στοιχεία επί των στηρίξεων
- Περί σφαιροποιΐας
Παλίμψηστο του Αρχιμήδη[]
Το κύριο έγγραφο που περιέχει το έργο του Αρχιμήδη είναι το Παλίμψηστο του Αρχιμήδη. Το 1906, ο Δανός καθηγητής Johan Ludvig Heiberg επισκέφθηκε την Κωνσταντινούπολη και εξέτασε περγαμηνή(από δέρμα κατσίκας), γραμμένη τον 13ο μ.Χ. αιώνα, η οποία περιείχε 174 σελίδες λειτουργικών κειμένων. Τελικά ανακάλυψε ότι η περγαμηνή ήταν ένα παλίμψηστο, δηλαδή ένα έγγραφο με κείμενο το οποίο είχε γραφεί πάνω σε μια σβησμένη παλιά εργασία. Τα παλίμψηστα δημιουργούνταν ξαίνοντας το μελάνι από τα αρχικά έργα των περγαμηνών και με την επαναχρησιμοποίηση τους. Αυτή ήταν μια συνηθισμένη πρακτική στον Μεσαίωνα, καθώς η περγαμηνή ήταν αρκετά ακριβή. Τα παλιότερα έργα στο παλίμψηστο αναγνωρίστηκαν από τους μελετητές τον 10ο αιώνα μ.Χ., ως αντίγραφα από προηγούμενες άγνωστες πραγματείες του Αρχιμήδη.[57] Η περγαμηνή, πριν να πωληθεί σε ιδιώτη συλλέκτη το 1920, ήταν για εκατοντάδες χρόνια σε μια μοναστηριακή βιβλιοθήκη στην Κωνσταντινούπολη. Στις 29 Οκτωβρίου 1998, πωλήθηκε σε δημοπρασία σε έναν ανώνυμο αγοραστή για 2 εκατομμύρια δολάρια από τον οίκο Κρίστις, στη Νέα Υόρκη.[58] Το παλίμψηστο περιέχει επτά πραγματείες, συμπεριλαμβανομένου και του μοναδικού σωζόμενου αντιγράφου του έργου "Περί των επιπλεόντων σωμάτων" στην αρχαία ελληνική. Είναι η μοναδική γνωστή πηγή του έργου "Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος", που αναφέροταν στη Σούδα και θεωρούταν ότι είχε χαθεί οριστικά. Το "Οστομάχιον" επίσης ήταν στο παλίμψηστο, με μια πιο πλήρη ανάλυση του puzzle, σε σχέση με ό,τι είχε βρεθεί σε προηγούμενα κείμενα. Το παλίμψηστο είναι τώρα αποθηκευμένο στο Walters Art Museum της Βαλτιμόρης, Μέριλαντ, όπου υποβάλλεται σε διάφορων ειδών σύγχρονες δοκιμές, όπως η χρήση υπεριώδους ακτινοβολίας και ακτίνων Χ, έτσι ώστε να διαβαστεί το αρχικό κείμενο.[59]
Οι πραγματείες του Αρχιμήδη στο Παλίμψηστο είναι: Περί επιπέδων ισορροπιών, Περί ελίκων, Κύκλου μέτρησις, Περί σφαίρας και κυλίνδρου, Περί των επιπλεόντων σωμάτων, Περί μηχανικών θεωρημάτων προς Ερατοσθένη έφοδος και Οστομάχιον.
Κληρονομία[]
- Υπάρχει ένας κρατήρας στη Σελήνη με το όνομα του Αρχιμήδη (29.7° Β, 4.0° Δ)προς τιμήν του, καθώς και μια σεληνιακή οροσειρά, τα βουνά του Αρχιμήδη (25.3° Β, 4.6° Δ).[60]
- Ο αστεροειδής της κύριας ζώνης αστεροειδών, με προσωρινή ονομασία 1987 SL7, πήρε το όνομα 3600 Αρχιμήδης από αυτόν.[61]
- Το μετάλλιο Fields για εξαιρετικές επιδόσεις στα μαθηματικά φέρει ένα πορτρέτο του Αρχιμήδη, μαζί με ένα σκάλισμα απεικονίζει την απόδειξη του στη σφαίρα και τον κύλινδρο.Η επιγραφή περί την κεφαλή του Αρχιμήδους είναι ένα απόσπασμα που αποδίδεται σε αυτόν, και γράφει στα λατινικά: "Transire suum pectus mundoque potiri" (Ανέβα επάνω από τον εαυτό σου και κατέκτησε τον κόσμο).[62]
- Ο Αρχιμήδης έχει αποτυπωθεί στα γραμματόσημα που εκδίδονται από την Ανατολική Γερμανία (1973), Ελλάδα (1983), Ιταλία (1983), τη Νικαράγουα (1971), Σαν Μαρίνο (1982), και την Ισπανία (1963).[63]
- Το επιφώνημα του Εύρηκα! που αποδίδεται στον Αρχιμήδη είναι το σύνθημα της πολιτείας της Καλιφόρνια. Στην περίπτωση αυτή η λέξη αναφέρεται στην ανακάλυψη του χρυσού κοντά στο Σάττερς Μιλ το 1848 που πυροδότησε τον πυρετό του χρυσού στην Καλιφόρνια.[64]
- Ένα κίνημα με πολιτική συμμετοχή,που αποσκοπεί στην καθολική πρόσβαση στην υγειονομική περίθαλψη στην αμερικανική πολιτεία του Όρεγκον έχει ονομαστεί το "Κίνημα Ο Αρχιμήδης», με επικεφαλής τον πρώην Κυβερνήτη του Όρεγκον John Kitzhaber.[65]
Σημειώσεις[]
a. Στο πρόλογο του Οι Σπείρες απευθυνόμενος στον Δοσίθεο από το Πηλούσιο, ο Αρχιμήδης λέει ότι "πολλά χρόνια πέρασαν από το θάνατο του Κόνωνα".Ο Κόνων ο Σάμιος έζησε το 280-220 π.Χ., κάτι που υπονοεί ότι ο Αρχιμήδης ήταν μεγαλύτερης ηλικίας όταν έγραψε μερικά από τα έργα του.
b. Οι πραγματείες του Αρχιμήδη που γνωρίζουμε μέσα από έργα άλλων συγγραφέων είναι:Κατασκευές πάνω σε σφαίρα και μια εργασία πάνω στα πολύεδρα που την αναφέρει ο Πάππος ο Αλεξανδρινός· Κατοπτρικά, μια εργασία στην οπτική που αναφέρεται από τον Θέωνα τον Αλεξανδρέα· Αρχές, όπου απευθύνεται στον Ζεύξιππο και του εξηγεί το αριθμητικό σύστημα που χρησιμοποιεί στα Ψαμμίτη· Ισσοροπίες και μοχλοί, Κέντρα βαρύτητας, Ημερολόγιο. Από τα σωζόμενα έργα του Αρχιμήδη, ο T. L. Heath κάνει μια υπόθεση για τη σειρά με την οποία γράφτηκαν: Κέντρα βάρους επιπέδων I, Ο τετραγωνισμός της παραβολής, Κέντρα βάρους επιπέδων II, Περί σφαίρας και κυλίνδρου I, II, Οι Σπείρες, Περί σφαιροειδέων και κωνοειδέων, Περί επιπλεόντων σωμάτων I, II, Κύκλου μέτρησις, Ψαμμίτης.
c. Πρότυπο:Note labelΚαρλ Μπέντζαμιν Μπόγιερ A History of Mathematics(Μία Ιστορία Μαθηματικών) (1991) ISBN 0-471-54397-7 "'Αραβες μελετητές μας πληροφορούν, ότι ο γνωστός τύπος για τον υπολογισμό του εμβαδού ενός τριγώνου,συναρτήσει των τριών πλευρών του(ευρέως γνωστός ως τύπος του 'Ηρωνα) k = √(s(s − a)(s − b)(s − c)),όπου s η ημιπερίμετρος-ήταν γνωστός στον Αρχιμήδη αρκετούς αιώνες,πριν τη γέννηση του Ήρωνα.Επίσης,'Αραβες μελετητές αποδίδουν στον Αρχιμήδη το «θεώρημα για τη σπασμένη χορδή»....Ο Αρχιμήδης αναφέρεται από τους Άραβες πως έχει δώσει αρκετές αποδείξεις αυτού του θεωρήματος."
d. Πρότυπο:Note label"Ήταν σύνηθες να αλείφουν τις γραμμές συναρμογής ή ακόμα και ολόκληρο το σκάφος με πίσσα ή με πίσσα και κερί". Στο έργο Νεκρικοὶ Διάλογοι, ο Λουκιανός αναφέρεται στην επικάλυψη των γραμμών συναρμογής των σκιφ (είδος πλοίου) με κερί, μια αναφορά σε πίσσα ή κερί.[66]
Εργογραφία[]
Οι σημαντικότερες συνεισφορές του στην Επιστήμη και ειδικότερα στα Μαθηματικά και την Φυσική είναι:
Υποσημειώσεις[]
- ↑ Archimedes (c.287 - c.212 BC). BBC History. http://www.bbc.co.uk/history/historic_figures/archimedes.shtml. Ανακτήθηκε την 2012-06-07.
- ↑ 2,0 2,1 Archimedes Death Ray: Testing with MythBusters. MIT. http://web.mit.edu/2.009/www//experiments/deathray/10_Mythbusters.html. Ανακτήθηκε την 2007-07-23.
- ↑ Calinger, Ronald (1999). A Contextual History of Mathematics. Prentice-Hall. σελ. 150. ISBN 0-02-318285-7. "Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity."
- ↑ Archimedes of Syracuse. The MacTutor History of Mathematics archive. Ιανουάριος 1999. http://www-history.mcs.st-and.ac.uk/Biographies/Archimedes.html. Ανακτήθηκε την 2008-06-09.
- ↑ O'Connor, J.J. and Robertson, E.F. (Φεβρουάριος 1996). A history of calculus. University of St Andrews. Αρχειοθετήθηκε από το πρωτότυπο στις 15 Ιουλίου 2007. http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/The_rise_of_calculus.html. Ανακτήθηκε την 2007-08-07.
- ↑ Bursill-Hall, Piers. Galileo, Archimedes, and Renaissance engineers. sciencelive with the University of Cambridge. http://www.sciencelive.org/component/option,com_mediadb/task,view/idstr,CU-MMP-PiersBursillHall/Itemid,30. Ανακτήθηκε την 2007-08-07.Πρότυπο:Dead link
- ↑ Archimedes – The Palimpsest. Walters Art Museum. Αρχειοθετήθηκε από το πρωτότυπο στις 2007-09-28. http://web.archive.org/web/20070928102802/http://www.archimedespalimpsest.org/palimpsest_making1.html. Ανακτήθηκε την 2007-10-14.
- ↑ T. L. Heath|Heath, T. L., Works of Archimedes, 1897
- ↑ Πλούταρχος. Βίοι Παράλληλοι - Μαρκέλλος 14. Wikisource. https://el.wikisource.org/wiki/%CE%92%CE%AF%CE%BF%CE%B9_%CE%A0%CE%B1%CF%81%CE%AC%CE%BB%CE%BB%CE%B7%CE%BB%CE%BF%CE%B9/%CE%9C%CE%AC%CF%81%CE%BA%CE%B5%CE%BB%CE%BB%CE%BF%CF%82#p14.
- ↑ O'Connor, J.J. και Robertson, E.F.. Archimedes of Syracuse. University of St Andrews. Αρχειοθετήθηκε από το πρωτότυπο στις 6 Φεβρουαρίου 2007. http://www-history.mcs.st-andrews.ac.uk/Biographies/Archimedes.html. Ανακτήθηκε την 2007-01-02.
- ↑ Πλούταρχος Βίοι Παράλληλοι - Μάρκελλος 19
- ↑ 12,0 12,1 Rorres, Chris. Death of Archimedes: Sources. Courant Institute of Mathematical Sciences. Αρχειοθετήθηκε από το πρωτότυπο στις 10 December 2006. http://www.math.nyu.edu/~crorres/Archimedes/Death/Histories.html. Ανακτήθηκε την 2007-01-02.
- ↑ Rorres, Chris. Tomb of Archimedes: Sources. Courant Institute of Mathematical Sciences. Αρχειοθετήθηκε από το πρωτότυπο στις 9 December 2006. http://www.math.nyu.edu/~crorres/Archimedes/Tomb/Cicero.html. Ανακτήθηκε την 2007-01-02.
- ↑ Για μία σύντομη επισκόπηση για την εντόπιση του τάφου, βλ. P.D. Scirpo, Στα ίχνη του Τάφου του Αρχιμήδη στις Συρακούσες, στο Σ.Α. Παϊπέτης - Χ. Γιαννοπούλου (επιμ.), «Πολιτισμική αλληλο-γονιμοποίηση Νότιας Ιταλίας και Δυτικής Ελλάδας μέσα από την Ιστορία». Πρακτικά του Διεθνούς Συνεδρίου (Πάτρα, 10-12/9/2007), Πάτρα, 2008, σσ. 68-81. Rorres, Chris. Tomb of Archimedes – Illustrations. Courant Institute of Mathematical Sciences. http://www.math.nyu.edu/~crorres/Archimedes/Tomb/TombIllus.html. Ανακτήθηκε την 2011-03-15.
- ↑ Πολύβιος Ιστορίαι, βιβλίο 8ο, κεφ. 2
- ↑ Casson, Lionel (1971). Ships and Seamanship in the Ancient World. Princeton University Press. ISBN 0-691-03536-9.
- ↑ Dalley, Stephanie. Oleson, John Peter. Sennacherib, Archimedes, and the Water Screw: The Context of Invention in the Ancient World. Technology and Culture Volume 44, Number 1, Ιανουάριος 2003 (PDF). http://muse.jhu.edu/journals/technology_and_culture/toc/tech44.1.html. Ανακτήθηκε την 2007-07-23.
- ↑ Rorres, Chris. Archimedes screw – Optimal Design. Courant Institute of Mathematical Sciences. http://www.cs.drexel.edu/~crorres/Archimedes/Screw/optimal/optimal.html. Ανακτήθηκε την 2007-07-23.
- ↑ An animation of an Archimedes screw
- ↑ SS Archimedes. wrecksite.eu. http://www.wrecksite.eu/wreck.aspx?636. Ανακτήθηκε την 2011-01-22.
- ↑ Rorres, Chris. Archimedes' Claw – Illustrations and Animations – a range of possible designs for the claw. Courant Institute of Mathematical Sciences. http://www.math.nyu.edu/~crorres/Archimedes/Claw/illustrations.html. Ανακτήθηκε την 2007-07-23.
- ↑ Carroll, Bradley W. Archimedes' Claw – watch an animation. Weber State University. Αρχειοθετήθηκε από το πρωτότυπο στις 13 August 2007. http://physics.weber.edu/carroll/Archimedes/claw.htm. Ανακτήθηκε την 2007-08-12.
- ↑ Ιππίας, 2 (παράβαλε Γαληνός, Περί κράσεων 3.2, που αναφέρει πυρεία, «δαυλούς») · Ανθέμιος ο Τραλλιανός, Περί παραδόξων μηχανημάτων 153 [Westerman].
- ↑ John Wesley. A Compendium of Natural Philosophy (1810) Chapter XII, Burning Glasses. Online text at Wesley Center for Applied Theology. Αρχειοθετήθηκε από το πρωτότυπο στις 2007-10-12. http://web.archive.org/web/20071012154432/http://wesley.nnu.edu/john_wesley/wesley_natural_philosophy/duten12.htm. Ανακτήθηκε την 2007-09-14.
- ↑ Πρότυπο:Cite news
- ↑ Bonsor, Kevin. How Wildfires Work. HowStuffWorks. Αρχειοθετήθηκε από το πρωτότυπο στις 14 July 2007. http://science.howstuffworks.com/wildfire.htm. Ανακτήθηκε την 2007-07-23.
- ↑ Fuels and Chemicals – Auto Ignition Temperatures
- ↑ TV Review: MythBusters 8.27 – President's Challenge. http://fandomania.com/tv-review-mythbusters-8-27-presidents-challenge/. Ανακτήθηκε την 2010-12-18.
- ↑ Rorres, Chris. The Law of the Lever According to Archimedes. Courant Institute of Mathematical Sciences. http://www.math.nyu.edu/~crorres/Archimedes/Lever/LeverLaw.html. Ανακτήθηκε την 2010-03-20.
- ↑ Clagett, Marshall (2001). Greek Science in Antiquity. Dover Publications. ISBN 978-0-486-41973-2. http://books.google.com/?id=mweWMAlf-tEC&pg=PA72&lpg=PA72&dq=archytas+lever&q=archytas%20lever. Ανακτήθηκε την 2010-03-20.
- ↑ Αναφέρεται από τον Πάππο στη Συναγωγή, Βιβλίο VIII
- ↑ Πλούταρχος Βίοι Παράλληλοι - Μάρκελλος 14
- ↑ Dougherty, F.C.; Macari, J.; Okamoto, C.. Pulleys. Society of Women Engineers. Αρχειοθετήθηκε από το πρωτότυπο στις 18 Ιουλίου 2007. http://www.swe.org/iac/lp/pulley_03.html. Ανακτήθηκε την 2007-07-23.
- ↑ Ancient Greek Scientists: Hero of Alexandria. Technology Museum of Thessaloniki. Αρχειοθετήθηκε από το πρωτότυπο στις 5 Σεπτεμβρίου 2007. http://www.tmth.edu.gr/en/aet/5/55.html. Ανακτήθηκε την 2007-09-14.
- ↑ Κικέρων. De re publica 1.xiv §21. thelatinlibrary.com. http://www.thelatinlibrary.com/cicero/repub1.shtml#21. Ανακτήθηκε την 2007-07-23.
- ↑ Κικέρων. De re publica Πλήρες κείμενο στα αγγλικά από το Gutenberg.org. Project Gutenberg. Αρχειοθετήθηκε από το πρωτότυπο στις 29 September 2007. http://www.gutenberg.org/etext/14988. Ανακτήθηκε την 2007-09-18.
- ↑ Rorres, Chris. Spheres and Planetaria. Courant Institute of Mathematical Sciences. http://www.math.nyu.edu/~crorres/Archimedes/Sphere/SphereIntro.html. Ανακτήθηκε την 2007-07-23.
- ↑ Πρότυπο:Cite news
- ↑ Πλούταρχος Βίοι Παράλληλοι - Μάρκελλος, 17
- ↑ Heath, T.L.. Archimedes on measuring the circle. math.ubc.ca. http://www.math.ubc.ca/~cass/archimedes/circle.html. Ανακτήθηκε την 2012-10-30.
- ↑ Kaye, R.W.. Archimedean ordered fields. web.mat.bham.ac.uk. http://web.mat.bham.ac.uk/R.W.Kaye/seqser/archfields. Ανακτήθηκε την 2009-11-07.
- ↑ Quoted in Heath, T.L. Works of Archimedes, Dover Publications, ISBN 0-486-42084-1.
- ↑ McKeeman, Bill. The Computation of Pi by Archimedes. Matlab Central. http://www.mathworks.com/matlabcentral/fileexchange/29504-the-computation-of-pi-by-archimedes/content/html/ComputationOfPiByArchimedes.html#37. Ανακτήθηκε την 2012-10-30.
- ↑ Carroll, Bradley W. The Sand Reckoner. Weber State University. Αρχειοθετήθηκε από το πρωτότυπο στις 13 August 2007. http://physics.weber.edu/carroll/Archimedes/sand.htm. Ανακτήθηκε την 2007-07-23.
- ↑ Encyclopedia of ancient Greece By Wilson, Nigel Guy p. 77 ISBN 0-7945-0225-3 (2006)
- ↑ Editions of Archimedes' Work. Brown University Library. Αρχειοθετήθηκε από το πρωτότυπο στις 8 August 2007. http://www.brown.edu/Facilities/University_Library/exhibits/math/wholefr.html. Ανακτήθηκε την 2007-07-23.
- ↑ Van Helden, Al. The Galileo Project: Hydrostatic Balance. Rice University. Αρχειοθετήθηκε από το πρωτότυπο στις 5 September 2007. http://galileo.rice.edu/sci/instruments/balance.html. Ανακτήθηκε την 2007-09-14.
- ↑ Heath, T.L.. The Works of Archimedes (1897). The unabridged work in PDF form (19 MB). Archive.org. Αρχειοθετήθηκε από το πρωτότυπο στις 6 October 2007. http://www.archive.org/details/worksofarchimede029517mbp. Ανακτήθηκε την 2007-10-14.
- ↑ Krumbiegel, B. and Amthor, A. Das Problema Bovinum des Archimedes, Historisch-literarische Abteilung der Zeitschrift Für Mathematik und Physik 25 (1880) pp. 121–136, 153–171.
- ↑ English translation of The Sand Reckoner. University of Waterloo. Αρχειοθετήθηκε από το πρωτότυπο στις 11 August 2007. http://www.math.uwaterloo.ca/navigation/ideas/reckoner.shtml. Ανακτήθηκε την 2007-07-23.
- ↑ Πρότυπο:Cite news
- ↑ Ed Pegg Jr. (November 17, 2003). The Loculus of Archimedes, Solved. Mathematical Association of America. Αρχειοθετήθηκε από το πρωτότυπο στις 19 May 2008. http://www.maa.org/editorial/mathgames/mathgames_11_17_03.html. Ανακτήθηκε την 2008-05-18.
- ↑ Rorres, Chris. Archimedes' Stomachion. Courant Institute of Mathematical Sciences. Αρχειοθετήθηκε από το πρωτότυπο στις 26 October 2007. http://math.nyu.edu/~crorres/Archimedes/Stomachion/intro.html. Ανακτήθηκε την 2007-09-14.
- ↑ Graeco Roman Puzzles. Gianni A. Sarcone and Marie J. Waeber. Αρχειοθετήθηκε από το πρωτότυπο στις 14 May 2008. http://www.archimedes-lab.org/latin.html#archimede. Ανακτήθηκε την 2008-05-09.
- ↑ Archimedes' Book of Lemmas. cut-the-knot. Αρχειοθετήθηκε από το πρωτότυπο στις 11 July 2007. http://www.cut-the-knot.org/Curriculum/Geometry/BookOfLemmas/index.shtml. Ανακτήθηκε την 2007-08-07.
- ↑ Ωστόσο, η πρώτη αξιόπιστη αναφορά στον τύπο δίνεται από τον |Ήρωνα τον Αλεξανδρέα τον 1ο μ.Χ. αιώνα.
- ↑ Miller, Mary K. (March 2007). Reading Between the Lines. Smithsonian Magazine. Αρχειοθετήθηκε από το πρωτότυπο στις 19 Ιανουαρίου 2008. http://www.smithsonianmag.com/science-nature/archimedes.html. Ανακτήθηκε την 2008-01-24.
- ↑ Πρότυπο:Cite news
- ↑ Πρότυπο:Cite news
- ↑ Friedlander, Jay and Williams, Dave. Oblique view of Archimedes crater on the Moon. NASA. Αρχειοθετήθηκε από το πρωτότυπο στις 19 August 2007. http://nssdc.gsfc.nasa.gov/imgcat/html/object_page/a15_m_1541.html. Ανακτήθηκε την 2007-09-13.
- ↑ Planetary Data System. NASA. Αρχειοθετήθηκε από το πρωτότυπο στις 12 October 2007. http://starbrite.jpl.nasa.gov/pds-explorer/index.jsp?selection=othertarget&targname=3600%20ARCHIMEDES. Ανακτήθηκε την 2007-09-13.
- ↑ Fields Medal. International Mathematical Union. Αρχειοθετήθηκε από το πρωτότυπο στις July 1, 2007. http://web.archive.org/web/20070701033751/http://www.mathunion.org/medals/Fields/AboutPhotos.html. Ανακτήθηκε την 2007-07-23.
- ↑ Rorres, Chris. Stamps of Archimedes. Courant Institute of Mathematical Sciences. http://math.nyu.edu/~crorres/Archimedes/Stamps/stamps.html. Ανακτήθηκε την 2007-08-25.
- ↑ California Symbols. California State Capitol Museum. Αρχειοθετήθηκε από το πρωτότυπο στις 12 October 2007. http://www.capitolmuseum.ca.gov/VirtualTour.aspx?content1=1278&Content2=1374&Content3=1294. Ανακτήθηκε την 2007-09-14.
- ↑ The Archimedes Movement. http://www.archimedesmovement.org/.
- ↑ Casson, Lionel (1995). Ships and seamanship in the ancient world. Baltimore: The Johns Hopkins University Press. σελ. 211–212. ISBN 978-0-8018-5130-8. http://books.google.com/books?id=sDpMh0gK2OUC&pg=PA18&dq=why+were+homer%27s+ships+black#v=onepage&q=why%20were%20homer's%20ships%20black&f=false.
Εσωτερική Αρθρογραφία[]
- Αρχιμήδειο Παλίμψηστο
- Αρχιμήδειος Δρέπανος
- Αρχιμήδεια Ιδιότητα
- Αρχή Αρχιμήδη για την πλευστότητα
- Στερεό Αρχιμήδη
- Αρχύτας \Τάρας \Αρχύτας ο Ταραντίνος
- Διοκλής ο Αλεξανδρεύς
- Αρχιμήδειο Τηλεβόλο
- Τετραγωνισμός Κύκλου
- Συρακουσία (πλοίο)
- Βιτρούβιος
- Μαθηματικοί Αρχαίας Εποχής
- Μαθηματικά
Βιβλιογραφία[]
- Τάσιος, Θεοδόσιος Π.: «Το αντιτεχνοκρατικό σύνδρομο του Αρχιμήδη». Ελληνική Φιλοσοφική Επιθεώρηση, τόμ. 5 (1988), σσ. 174-181.
- Φίλη, Χριστίνα: «Πυθαγόρας, Αρχιμήδης και ινδικές μαθηματικές θεωρίες», Φιλοσοφία 15-16 (1985-86), 156-171
- Σ.Α. Παϊπέτης - M. Ceccarelli (eds.): «The Genius of Archimedes. 23 Centuries of Influence on the Fields of Mathematics, Science, and Engineering.». Proceedings of the International Symposium (Syracuse, 8-10/6/2010), Dordrecht 2010.
- Ball, W.W. Rouse (1960) [1908]. A Short Account of the History of Mathematics (4th ed.). Dover Publications. pp. 50–62. ISBN 0486206300.
- Boyer, Carl B. (1991). A History of Mathematics (2nd ed.). John Wiley & Sons, Inc.. ISBN 0471543977.
- Heath, Thomas L. (1981). A History of Greek Mathematics, 2 Vols. New York: Dover Publications. ISBN 0486240738 / ISBN 0486240746.
- Struik, Dirk J. (1967). A Concise History of Mathematics. Dover Publications. ISBN 486-60255-9.
Ιστογραφία[]
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)


