Διαταρακτική Θεωρία

Θεωρία Διαταραχών

Perturbation theory, Quantum perturbation theory, Field Theory, List of quantum field theories

Επιστημονική Θεωρία

---

Φυσικές Θεωρίες
Χημικές Θεωρίες
Γεωλογικές Θεωρίες
Βιολογικές Θεωρίες
Οικονομικές Θεωρίες

Επιστημονική Θεωρία
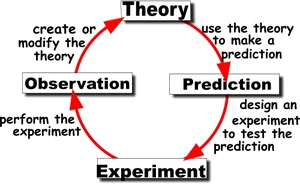
Φυσική Θεωρία
Χημική Θεωρία
Γεωλογική Θεωρία
Βιολογική Θεωρία
Οικονομική Θεωρία

Επιστημονική Θεωρία

Επιστημονική Θεωρία

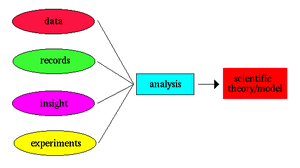
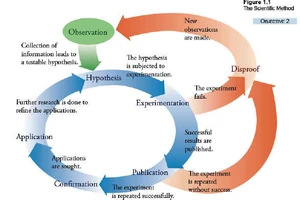
- Μια Φυσική Θεωρία.

Ετυμολογία

Η ονομασία "διαταρακτική" σχετίζεται ετυμολογικά με την λέξη "διαταραχή".

Εισαγωγή

Η θεωρία διαταραχών αποτελεί μία μαθηματική μέθοδο της Κβαντικής Μηχανικής που χρησιμοποιείται για τη περιγραφή περίπλοκων συστημάτων χρησιμοποιώντας ως "βάση περιγραφής" ένα απλούστερο, ακριβώς επιλύσιμο σύστημα.

Η βασική ιδέα πίσω από τη θεωρία διαταραχών είναι η εξής:

Δεδομένης μιας Χαμιλτονιανής με γνωστές ιδιοσυναρτήσεις και ιδιοτιμές, προσθέτουμε σταδιακά «μικρές» διορθώσεις («διαταραχές») οι οποίες έχουν υπολογίσιμες συνέπειες στις αδιατάρακτες ιδιοσυναρτήσεις και ιδιοτιμές της.

Έτσι, λοιπόν, ένα περίπλοκο σύστημα μπορεί να μελετηθεί με βάση ένα ακριβώς επιλύσιμο σύστημα.

Η κβαντική θεωρία διαταραχών χωρίζεται σε δύο βασικές κατηγορίες:

• Την χρονοανεξάρτητη θεωρία διαταραχών (γνωστή και ως θεωρία διαταραχών των Ρέιλι-Schrodinger από τους δύο πρωτοπόρους της θεωρίας)
• Την χρονοεξαρτημένη θεωρία διαταραχών

Χρονοανεξάρτητη Θεωρία Διαταραχών

Η χρονοανεξάρτητη θεωρία διαταραχών ασχολείται με στατικές Χαμιλτονιανές, δηλαδή ανεξάρτητες του χρόνου.

Υποθέτοντας ότι έχουμε ένα ακριβώς επιλύσιμο σύστημα με (χρονοανεξάρτητη) Χαμιλτονιανή Η⁽⁰⁾ και γνωστές ιδιοσυναρτήσεις και ιδιοτιμές |n⁽⁰⁾> και E_n⁽⁰⁾, προκύπτει το εξής ερώτημα:

Τι θα συμβεί αν στην αδιατάρακτη Χαμιλτονιανή προστεθεί ένας «μικρός» διαταρακτικός όρος της μορφής λΗ⁽¹⁾, όπου λ μία μικρή σταθερά;

Μαθηματικά, το προηγούμενο ερώτημα μεταφράζεται στην εξίσωση:

$H=H^{(0)} + \lambda H^{(1)} \ \ \$

Το ζητούμενο είναι να υπολογίσουμε την ποσόστητα μεταβολής των γνωστών ιδιοσυναρτήσεων και ιδιοτιμών του ακριβώς επιλύσιμου προβλήματος λόγω της προσθήκης της παραπάνω διαταραχής.

Η απάντηση στο ερώτημα προκύπτει από την ανάπτυξη των ιδιοτιμών της ενέργειας και των ιδιοτιμών σε μία δυναμοσειρά ως προς τη μεταβλητή λ, ήτοι:

$E_n=\lambda^{0}E^{(0)}_n+\lambda^{1}E^{(1)}_n+\lambda^{2}E^{(2)}_n+...$

$|n\rangle=\lambda^{0}|n^{(0)}\rangle+\lambda^{1}|n^{(1)}\rangle+\lambda^{2}|n^{(2)}\rangle+...$

Ο συντελεστής κάθε δύναμης του λ στα παραπάνω αναπτύγματα αντιστοιχεί στην αντίστοιχη τάξη διόρθωσης.

Παράδειγμα, αν λ=0 (δεν υπάρχει διαταρακτικός όρος στην ολική Χαμιλτονιανή), τότε H≡H⁽⁰⁾ και Ε_n ≡ E_n⁽⁰⁾.

Αντικαθιστώντας τα προηγούμενα αναπτύγματα στην εξίσωση Schrodinger:

$H|n\rangle=E_n |n\rangle \Leftrightarrow \left( H^{(0)}+\lambda H^{(1)} \right) \left( |n^{(0)}\rangle+\lambda |n^{(1)}\rangle+\lambda^2 |n^{(2)}\rangle+... \right)=$

$= \left( E^{(0)}_n+\lambda^{1}E^{(1)}_n+\lambda^{2}E^{(2)}_n+... \right) \left( |n^{(0)}\rangle+\lambda |n^{(1)}\rangle+\lambda^2 |n^{(2)}\rangle+... \right)$

Η εξίσωση των όμοιων δυνάμεων του λ καταλήγει στο παρακάτω σύστημα εξισώσεων:

$\begin{align} H^{(0)}|n^{(0)}\rangle &=E_n^{(0)}|n^{(0)}\rangle \\ H^{(0)}|n^{(1)}\rangle+H^{(1)}|n^{(0)}\rangle &=E_n^{(0)}|n^{(1)}\rangle+E_n^{(1)}|n^{(0)}\rangle \\ H^{(0)}|n^{(2)}\rangle+H^{(1)}|n^{(1)}\rangle &=E_n^{(0)}|n^{(2)}\rangle+E_n^{(1)}|n^{(1)}\rangle+E_n^{(2)}|n^{(0)}\rangle \\ &\vdots \end{align}$

Κάθε μία από τις παραπάνω εξισώσεις (με εξαίρεση την πρώτη, η οποία είναι η εξίσωση Schrodinger για το ακριβώς επιλύσιμο πρόβλημα) είναι δυνατόν να προσδιορίσει την τάξη διόρθωσης στις ιδιοτιμές και ιδιοσυναρτήσεις στην οποία αντιστοιχεί.

Διορθώσεις 1ης τάξης

Ο υπολογισμός των διορθώσεων πρώτης τάξης έχει ως αφετηρία την εξίσωση

$H^{(0)}|n^{(1)}\rangle+H^{(1)}|n^{(0)}\rangle =E_n^{(0)}|n^{(1)}\rangle+E_n^{(1)}|n^{(0)}\rangle$

Το ζητούμενο είναι ο υπολογισμός των ποσοτήτων E_n⁽¹⁾ και |n⁽¹⁾> συναρτήσει των αντίστοιχων ιδιοσυναρτήσεων και ιδιοτιμών του ακριβώς επιλύσιμου προβλήματος. Υπό την προϋπόθεση ότι οι διορθώσεις πρώτης τάξης στις ιδιοσυναρτήσεις, |n⁽¹⁾>, μπορούν να αναπτυχθούν σε μία δυναμοσειρά ως προς τις γνωστές ιδιοσυναρτήσεις |n⁽⁰⁾>, είναι δυνατόν να δειχθεί ότι

$E_n^{(1)}=\langle n^{(0)}|H^{(1)}|n^{(0)}\rangle, \ \ \ |n^{(1)}\rangle=\sum_{m\ne n}\frac{H^{(1)}_{mn}}{E_n^{(0)}-E_m^{(0)}} \ |m^{(0)}\rangle$

Το αποτέλεσμα αυτό ισχύει μόνο υπό την προϋπόθεση ότι το ενεργειακό φάσμα της αδιατάρακτης Χαμιλτονιανής H⁽⁰⁾ είναι μη εκφυλισμένο.

Διορθώσεις 2ης τάξης

Οι διορθώσεις δεύτερης τάξης έχουν ως αφετηρία την εξίσωση

$H^{(0)}|n^{(2)}\rangle+H^{(1)}|n^{(1)}\rangle = E_n^{(0)}|n^{(2)}\rangle+E_n^{(1)}|n^{(1)}\rangle+E_n^{(2)}|n^{(0)}\rangle$

Όπως και στην περίπτωση των διορθώσεων πρώτης τάξης, οι διορθώσεις δεύτερης τάξης στις ιδιοσυναρτήσεις και τις ιδιοτιμές του αδιατάρακτου προβλήματος είναι δυνατόν να υπολογισθούν υπό την προϋπόθεση ότι οι διορθώσεις δεύτερης τάξης των ιδιοσυναρτήσεων μπορούν να αναπτυχθούν σε δυναμοσειρά ως προς τις αδιατάρακτες ιδιοσυναρτήσεις. Το τελικό αποτέλεσμα είναι το εξής:

$E^{(2)}_n=\sum_{m\ne n}\frac{\left| \langle m^{(0)} | H^{(1)} | n^{(0)} \rangle \right|^2}{E_n^{(0}-E_m^{(0)}}$

$|n^{(2)}\rangle=\sum_{i\ne n}\sum_{j\ne n}\frac{\langle j^{(0)}|H^{(1)}|n^{(0)}\rangle \langle i^{(0)}|H^{(1)}|j^{(0)}\rangle}{\left(E^{(0)}_{n}-E^{(0)}_{j}\right)\left(E^{(0)}_{n}-E^{(0)}_{i}\right)}|i^{(0)}\rangle-\sum_{i\ne n}\frac{\langle n^{(0)}|H^{(1)}|n^{(0)}\rangle \langle i^{(0)}|H^{(1)}|n^{(0)}\rangle}{\left(E_n^{(0)}-E_i^{(0)}\right)^2}|i^{(0)}\rangle$

Εσωτερική Αρθρογραφία

• Αδιαταρακτική Θεωρία
• Κβαντικός Αρμονικός Ταλαντωτής
• Ηλιοειδές Άτομο
• Φαινόμενο Zeeman
• Φαινόμενο Stark
• Λεπτή Υφή, Υπέρλεπτη Υφή
• Φυσικό Πεδίο
• Φυσική Θεωρία
• Κλασσική Πεδιακή Θεωρία
• Σχετικιστική Πεδιακή Θεωρία
• Κβαντική Πεδιακή Θεωρία
• Μη-Διαταρακτική Συνάρτηση
• Μη-Διαταρακτική Επανακανονισιμότητα ( = nonperturbative renormalizability)

Βιβλιογραφία

• Τραχανάς Στέφανος, Κβαντομηχανική Ι, Πανεπιστημιακές Εκδόσεις Κρήτης 2009
• Τραχανάς Στέφανος, Κβαντομηχανική ΙΙ, Πανεπιστημιακές Εκδόσεις Κρήτης 2009

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---