Επίπεδο

Επίπεδον

Plane

Δισδιάστατος Χώρος

Επίπεδο

Τεμνόμενα ΕπίπεδαΆνθρωπος

Τεμνόμενα Επίπεδα

Παράλληλα Επίπεδα

Συμπίπτοντα Επίπεδα

Επίπεδο
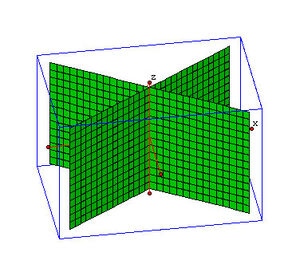
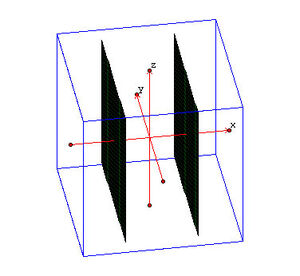
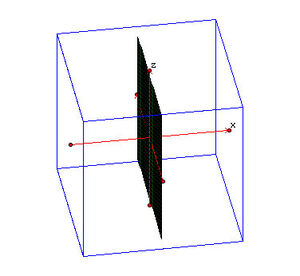
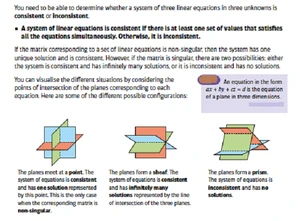
Τομή

Εγγύτατο (osculating) Επίπεδο
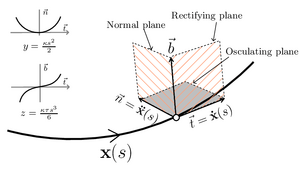
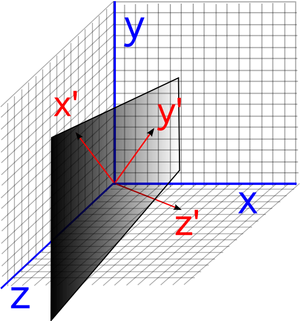
Ανορθωτικό (rectifying) Επίπεδο
Κάθετο (normal) Επίπεδο

- Ένα Γεωμετρικό Σχήμα.

Στη Ευκλείδεια Γεωμετρία το επίπεδο είναι μία από τις βασικές γεωμετρικές έννοιες.

Ετυμολογία

Η ονομασία "Επίπεδο" σχετίζεται ετυμολογικά με την λέξη "πεδίο".

Εισαγωγή

Το επίπεδο θεωρείται συνήθως αρχική έννοια της Γεωμετρίας, δηλαδή δεν ορίζεται με βάση άλλες στοιχειωδέστερες έννοιες, αν και σε κάποιες προσεγγίσεις της γεωμετρίας δεν είναι έτσι, όπως για παράδειγμα στην Αναλυτική Γεωμετρία όπου ορίζεται με βάση την έννοια του σημείου. Ιδιαίτερα όταν εργαζόμαστε στη δισδιάστατη Ευκλείδεια Γεωμετρία το επίπεδο αναφέρεται σε ολόκληρο το χώρο.

Διαισθητικά η έννοια του επιπέδου μπορεί να περιγραφεί ως μια εντελώς ίσια (δηλ. χωρίς κυρτότητα ή κοιλότητα) και λεία (δηλ. χωρίς «όρη» ή «κοιλάδες») επιφάνεια που έχει μηδενικό όγκο και καταλαμβάνει τις δύο μόνο διαστάσεις του τρισδιάστατου Χώρου. Επεκτείνεται απεριόριστα προς τις δύο διευθύνσεις. Δύο παράλληλα επίπεδα έχουν την ιδιότητα ότι ποτέ δεν τέμνονται, όσο και αν τα επεκτείνουμε. Επιπλέον, δύο επίπεδα μπορούν να εφαρμόσουν ακριβώς, ακόμα και όταν το ένα κινείται κατά την έκταση του άλλου.

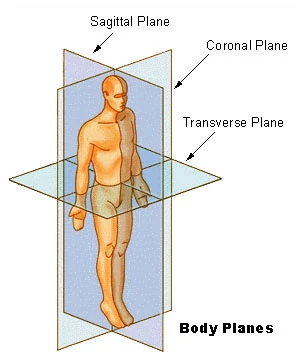
Μακροσκοπικές επιφάνειες ή αντικείμενα που συνήθως μοντελοποιούνται ή νοούνται ως επίπεδες επιφάνειες είναι οι τοίχοι, τα ταβάνια, και τα πατώματα ενός απλού σπιτιού, η πάνω επιφάνεια ενός τραπεζιού, ο πίνακας μίας σχολικής αίθουσας.

Περιγραφή του επιπέδου

Αξιωματική γεωμετρία

Σχεδόν σε κάθε γεωμετρία ισχύουν τα εξής που αφορούν το επίπεδο:

• Αν δύο σημεία που ανήκουν σε ένα επίπεδο ορίζουν μία ευθεία, τότε αυτή ανήκει εξ ολοκλήρου στο επίπεδο.
• Από τρία σημεία διέρχεται μοναδικό επίπεδο.
• Δύο ευθείες που ανήκουν στο ίδιο επίπεδο ταυτίζονται, τέμνονται ή είναι παράλληλες. Δε μπορούν να είναι ασύμβατες.
• Δύο επίπεδα που έχουν τουλάχιστον ένα κοινό σημείο ταυτίζονται ή τέμνονται κατά μήκος μιας ευθείας.
• Κάθε επίπεδο χωρίζει το χώρο σε τρεις περιοχές, ή ισοδύναμα δύο σημεία που δεν ανήκουν στο επίπεδο βρίσκονται είτε στο ίδιο μέρος του επιπέδου ή εκατέρωθέν του.
• Ένα επίπεδο έχει τρία τουλάχιστον σημεία που δεν βρίσκονται στην ίδια ευθεία και ένα σημείο έξω από το επίπεδο.
• Ένα επίπεδο μπορεί να προεκταθεί απεριόριστα.

Αναλυτική Γεωμετρία

Σε τρισδιάστατο ορθοκανονικό Σύστημα Αναφοράς ένα επίπεδο περιγράφεται από την εξίσωση:

${\frac {x}{a}}+{\frac {y}{b}}+{\frac {z}{c}}=1$

Επίσης μπορεί να θεωρηθεί ως ο Γεωμετρικός Χώρος που αντιστοιχεί σε αυτήν τη συνθήκη:

$(\mathrm {P} -\Pi )\delta =0$

Όπου Ρ το εφαρμοστό διάνυσμα θέσης τυχαίου σημείου του χώρου, Π το εφαρμοστό διάνυσμα θέσης ενός σημείου του χώρου και δ ένα διάνυσμα που λέγεται κάθετο διάνυσμα του επιπέδου. Οι αρχές των εφαρμοστών διανυσμάτων είναι η αρχή των αξόνων.

Το διάνυσμα Ρ-Π είναι ένα διάνυσμα του οποίου και τα δύο σημεία ανήκουν στο οριζόμενο επίπεδο, άρα ανήκει εξολοκλήρου στο επίπεδο.

Από τη σχέση προκύπτει ότι αυτό το διάνυσμα και το δ είναι κάθετα μεταξύ τους, άρα το δ δίδει στο επίπεδο έναν συγκεκριμένο προσανατολισμό. Ο προσδιορισμός του επιπέδου ολοκληρώνεται με το εφαρμοστό διάνυσμα Π, το οποίο τοποθετεί το ελεύθερο επίπεδο σε συγκεκριμένη θέση. Το Π ανήκει στο επίπεδο, αφού $\Pi -\Pi ={\vec {0}}$

Γραμμική Άλγεβρα

Το επίπεδο είναι η λύση γραμμικών εξισώσεων της μορφής αχ + βψ + γω = 0, όπου α, β, γ παράμετροι τέτοιες, ώστε |α|+|β|+|γ|$\ne$0, δηλαδή να μην είναι όλες μηδέν.

Αν σε μία εξίσωση αυτής της μορφής είναι α=β=γ=0, τότε η λύση του συστήματος είναι όλος ο τρισδιάστατος χώρος.

Εσωτερική Αρθρογραφία

• επιπεδότητα
• Χώρος
• επιφάνεια
• Ζεύγος Επιπέδων

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---