Ετικέτα: επεξεργασία κώδικα 2017 |
Χωρίς σύνοψη επεξεργασίας Ετικέτα: επεξεργασία κώδικα 2017 |
||
| (13 ενδιάμεσες αναθεωρήσεις από τον ίδιο χρήστη δεν εμφανίζεται) | |||
| Γραμμή 10: | Γραμμή 10: | ||
| − | [[image: |
+ | [[image:Curvature-15-goog.png|thumb|300px|<center>[[Καμπυλότητα]] </center>]] |
| − | [[image:Curvature- |
+ | [[image:Curvature-wrinkles-01-goog.jpg|thumb|300px|<center>[[Καμπυλότητα]] </center>]] |
| − | [[ |
+ | [[image:Curvature-16-goog.png|thumb|300px|<center> [[Καμπυλότητα]] |
| + | ---- |
||
| ⚫ | |||
| + | Υπάρχουν πολλές ατραποί (καμπύλες) που μπορεί να ακολουθήσετε για να φθάσετε από ένα σημείο σε ένα άλλο. <br> |
||
| + | O Gauss (όπως η άποψή του διατυπώθηκε στο theorema egregium = αξιοσημείωτο θεώρημα ) <br> έλαβε υπ' όψη του όλες τις δυνατές επιλογές. <br> |
||
| + | Από οποιοδήποτε σημείο βρείτε τις δύο κορυφογραμμές <br> |
||
| + | (δηλ. την πλέον κοίλη και την πλέον κυρτή) <br>που μπορείτε να ακολουθήσετε <br>και πολλαπλασιάστε τις καμπυλότητές τους τότε <br>το γινόμενο τους θα είναι η κατά Gauss καμπυλότητα της επιφάνειας. |
||
| + | </center>]] |
||
| + | [[image:Earth-Projections-01-goog.png|thumb|300px|<center>[[Προβολή]] <br>[[καμπυλότητα]]</center>]] |
||
| + | [[image:Surface-Curvature-01-goog.png|thumb|300px|<center>[[Επιφάνεια]] <br> [[Καμπυλότητα]] <br> [[Ιακωβιανή]] </center>]] |
||
| + | [[image:Curvature-03-goog.gif|thumb|300px|<center>[[Καμπυλότητα]] <br> [[Επιπεδότητα]] </center>]] |
||
| + | [[Image:Physicists-Wheeler-01-goog.jpg|thumb|300px|<center>[[Φυσική]] <br> [[Wheeler John|John Wheeler]] </center>]] |
||
| ⚫ | |||
| + | [[image:Point-extremal-Line-crest-01-goog.gif|thumb|300px|<center>[[κορυφογραμμή]] <br> [[Ακρότατο Σημείο]] </center>]] |
||
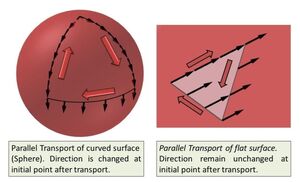
| + | [[image:Parallel-transport-02-goog.jpg|300px|thumb|<center>[[Παράλληλη Μεταφορά]] </center>]] |
||
| + | [[image:Curvature-cylinder-plane-01-goog.gif|thumb|300px|<center>[[Κύλινδρος]] <br>[[Επίπεδο \Σχήμα |Επίπεδο]] <br> [[Καμπυλότητα]] |
||
| + | ---- |
||
| + | ''When a surface has a [[Gaussian curvature]] of 0 at every [[point]],<br> then we say that the [[surface]] is Gaussian flat. <br>It can be shown that surfaces that are [[flatness |flat]]<br> with respect to Gaussian [[curvature]] can be constructed <br>by deforming a section of a plane without<br> [[tearing]], [[folding]], or [[stretching]] the plane. <br>For example, the [[cylinder]] is Gaussian flat because <br>it can be formed by rolling up a [[sheet]] of paper. ''</center>]] |
||
| + | [[image:Curvature-cylinder-plane-02-goog.png|thumb|300px|<center>[[Κύλινδρος]] <br>[[Επίπεδο \Σχήμα |Επίπεδο]] <br> [[Καμπυλότητα]]</center>]] |
||
| + | [[Image:Torus-curvature-01-goog.jpg|thumb|300px|<center>[[Τόρος]]<br> [[καμπυλότητα]]</center>]] |
||
- Μία [[Γεωμετρική Ιδιότητα]] |
- Μία [[Γεωμετρική Ιδιότητα]] |
||
| Γραμμή 58: | Γραμμή 75: | ||
*[http://el.wikipedia.org/wiki/Καμπυλότητα Ομώνυμο άρθρο στην Βικιπαίδεια] |
*[http://el.wikipedia.org/wiki/Καμπυλότητα Ομώνυμο άρθρο στην Βικιπαίδεια] |
||
*[http://www.livepedia.gr/index.php?title=Καμπυλότητα Ομώνυμο άρθρο στην Livepedia] |
*[http://www.livepedia.gr/index.php?title=Καμπυλότητα Ομώνυμο άρθρο στην Livepedia] |
||
| + | *[http://simplemindsimplemath.weebly.com/curvature_pizza.html pizza καμπυλότητα] |
||
| − | *[ ] |
||
| + | *[http://www.physics4u.gr/articles/2002/curvedspace.html physics4u.gr] |
||
| − | *[ ] |
||
{{Sciencepedia}} |
{{Sciencepedia}} |
||
Τελευταία αναθεώρηση της 09:26, 24 Φεβρουαρίου 2024
Καμπυλότης


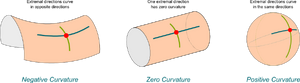
Υπάρχουν πολλές ατραποί (καμπύλες) που μπορεί να ακολουθήσετε για να φθάσετε από ένα σημείο σε ένα άλλο.
O Gauss (όπως η άποψή του διατυπώθηκε στο theorema egregium = αξιοσημείωτο θεώρημα )
έλαβε υπ' όψη του όλες τις δυνατές επιλογές.
Από οποιοδήποτε σημείο βρείτε τις δύο κορυφογραμμές
(δηλ. την πλέον κοίλη και την πλέον κυρτή)
που μπορείτε να ακολουθήσετε
και πολλαπλασιάστε τις καμπυλότητές τους τότε
το γινόμενο τους θα είναι η κατά Gauss καμπυλότητα της επιφάνειας.
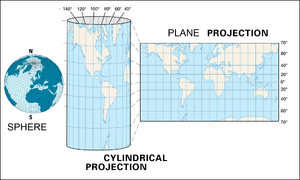
καμπυλότητα
Καμπυλότητα
Ιακωβιανή

Επιπεδότητα

John Wheeler
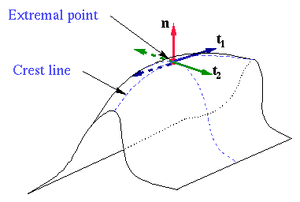
Ακρότατο Σημείο
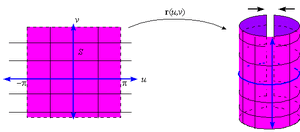
Επίπεδο
Καμπυλότητα
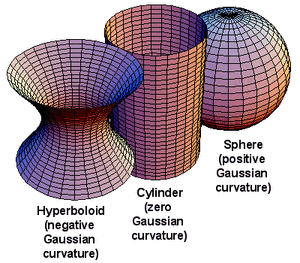
When a surface has a Gaussian curvature of 0 at every point,
then we say that the surface is Gaussian flat.
It can be shown that surfaces that are flat
with respect to Gaussian curvature can be constructed
by deforming a section of a plane without
tearing, folding, or stretching the plane.
For example, the cylinder is Gaussian flat because
it can be formed by rolling up a sheet of paper.
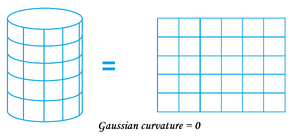
Επίπεδο
Καμπυλότητα
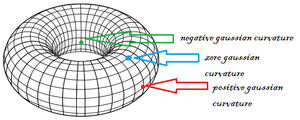
καμπυλότητα
- Μία Γεωμετρική Ιδιότητα
Ετυμολογία[]
Η ονομασία "Καμπυλότητα" σχετίζεται ετυμολογικά με την λέξη "καμπύλη".
Εισαγωγή[]
A piece of paper can be rolled into a cone, but can never wrap an apple without being torn or creased.
This can be explained, mathematically, by use of the Gaussian curvature.
The curvature of a geometry does not change as long as you don't tear/fold/distort it.
It can be
- positive, like a sphere;
- zero, like a plane; or
- negative, like a pringle.
One way to tell what kind of curvature there is, is to put a flat surface so it touches a point on the shape, and investigate how many pieces it is split into (shown in animation).
Another method would be to draw a triangle on the surface. If the angles add up to
- more than 180°, then there is positive curvature
- less then there is negative curvature.
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
- κυρτότητα, κοιλότητα
- Καμπυλότητα, ένα γεωμετρικό μέγεθος
- εκκεντρότητα
- Εκκεντρότητα, ένα γεωμετρικό μέγεθος
- επιπεδότητα
- Καμπύλος Χώρος (curved)
- Χώρος Riemann
- Χώρος Lobachevski
Βιβλιογραφία[]
Ιστογραφία[]
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)
