Κβαντικός Αριθμός
Κβαντικοί Αριθμοί
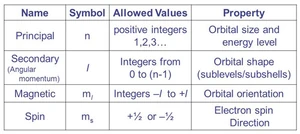
Κύριος Κβαντικός Αριθμός Αζιμουθιακός Κβαντικός Αριθμός Μαγνητικός Κβαντικός Αριθμός Σπινώδης Κβαντικός Αριθμός

- Ένα κβαντικό Φυσικό Μέγεθος.
Ετυμολογία[]
Η ονομασία "Κβαντικός" σχετίζεται ετυμολογικά με την λέξη "κβάντο".
Εισαγωγή[]
Οι κβαντικοί αριθμοί n και l, εμφανίστηκαν στην παλαιά κβαντική θεωρία των Bohr και Sommerfeld.
O κύριος κβαντικός αριθμός n περιελήφθηκε στο πρότυπο του Bohr αξιωματικά και αφορούσε την κβάντωση της στροφορμής, ενώ ο τροχιακός κβαντικός αριθμός εισήχθη μερικά έτη αργότερα από τον Sommerfeld ως διόρθωση για να δικαιολογήσει τις ελλειπτικές τροχιές.
Οι δύο αυτοί κβαντικοί αριθμοί επανεμφανίζονται στην θεωρητική – κβαντική αντιμετώπιση του θέματος του ατόμου του υδρογόνου και στην περίπτωση των ατόμων με πολλά ηλεκτρόνια.
Οι κβαντικοί αριθμοί είναι κάποιοι αριθμοί που αντιστοιχούν σε φυσικές ποσότητες όπως:
- η ενέργεια,
- η στροφορμή και
- η κβαντική ιδιοστροφορμή (spin)),
οι οποίες διατηρούνται σε ένα Κβαντικό Σύστημα με την πάροδο του χρόνου, και οι οποίοι περιγράφουν τις τιμές που λαμβάνουν οι αντίστοιχες αυτές φυσικές ποσότητες.
Από τη στιγμή που οποιοδήποτε κβαντικό σύστημα μπορεί να έχει έναν ή περισσότερους κβαντικούς αριθμούς, δεν έχει νόημα η παράθεση μιας λίστας με όλους τους κβαντικούς αριθμούς που υπάρχουν.
Μονοηλεκτρονικό Άτομο[]
Το σύνολο κβαντικών αριθμών που έχει μελετηθεί περισσότερο, είναι αυτό για ένα απλό ηλεκτρόνιο ενός ατόμου, όχι μόνο επειδή είναι χρήσιμο στη Χημεία, αλλά επειδή είναι ένα επιλύσιμο και ρεαλιστικό πρόβλημα, και, ως τέτοιο, βρίσκει ευρεία χρήση σε επιστημονικά βιβλία.
Στη μη σχετικιστική Κβαντική Φυσική, η Χαμιλτονιανή του συστήματος αυτού αποτελείται από την Κινητική Ενέργεια του ηλεκτρονίου και τη Δυναμική Ενέργεια που υπάρχει εξ' αιτίας της ηλεκτρικής δύναμης Coulomb ανάμεσα στα νουκλεόνια και το ηλεκτρόνιο.
Η κινητική ενέργεια μπορεί να χωριστεί σε δύο τμήματα, το πρώτο από τα οποία οφείλεται στη στροφορμή J, του ηλεκτρονίου περί τον ατομικό πυρήνα.
Από τη στιγμή που το δυναμικό Coulomb είναι σφαιρικά συμμετρικό, η Χαμιλτονιανή μετατίθεται με το τετράγωνο της στροφορμής J2. Το τετράγωνο της στροφορμής J2 μετατίθεται με οποιαδήποτε από τις συνιστώσες του διανύσματος της στροφορμής, που για λόγους σύμβασης επιλέγεται να είναι η Jz.
Αυτοί είναι και οι μόνοι τελεστές του προβλήματος οι οποίοι μετατίθενται, οπότε και έχουμε τρεις κβαντικούς αριθμούς.
Αυτοί είναι γνωστοί ως:
Κύριος Κβαντικός Αριθμός[]
Ο Κύριος Κβαντικός Αριθμός (n = 1, 2, 3, 4 ...), που εκφράζει την ιδιοτιμή της Χαμιλτονιανής H χωρίς το τμήμα της J2.
Ο αριθμός αυτός εξαρτάται μόνο από την απόσταση ανάμεσα στο ηλεκτρόνιο και τον πυρήνα του ατόμου (δηλαδή την ακτινική συντεταγμένη r).
Η μέση απόσταση αυξάνεται ανάλογα με το n, οπότε λέμε, κατά σύμβαση, ότι κβαντικές καταστάσεις με διαφορετικούς κύριους κβαντικούς αριθμούς ανήκουν σε διαφορετικούς "φλοιούς".
Όσο πιο μεγάλος είναι ο κύριος κβαντικός αριθμός ενός ηλεκτρονίου, τόσο πιο μεγάλη είναι η μέση απόστασή του από τον ατομικό πυρήνα.
Για παράδειγμα, εάν n=7, τότε το ηλεκτρόνιο βρίσκεται στον φλοιό Q, δηλαδή στον πιο μακρινό από τον ατομικό πυρήνα φλοιό.
Ο μέγιστος αριθμός ηλεκτρονίων που μπορούν να βρεθούν σε έναν φλοιό δίνεται από τον τύπο 2n2.
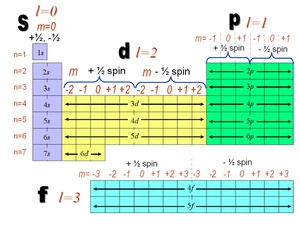
Αζιμουθιακός Κβαντικός Αριθμός[]
Ο Αζιμουθιακός Κβαντικός Αριθμός (l = 0, 1, ..., n-1) (επίσης γνωστός και ως κβαντικός αριθμός της στροφορμής ή τροχιακός κβαντικός αριθμός), δίνει την τροχιακή στροφορμή μέσω της σχέσης , όπου h είναι η σταθερά Planck.
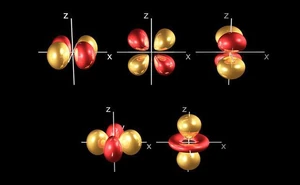
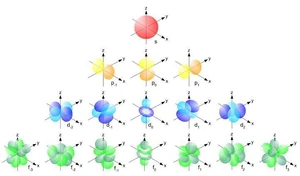
Ο αζιμουθιακός κβαντικός αριθμός είναι πολύ σημαντικός στη Χημεία, καθώς περιγράφει το σχήμα των ατομικών τροχιακών και επηρεάζει πολύ τη φύση των χημικών δεσμών.
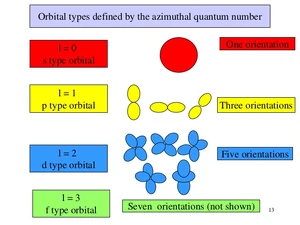
Συνήθως, χρησιμοποιείται η εξής ορολογία
- η περίπτωση l = 0 καλείται s-τροχιακό,
- η περίπτωση l = 1 καλείται p-τροχιακό,
- η περίπτωση l = 2 d-τροχιακό και
- η περίπτωση l = 3 f-τροχιακό.
Μαγνητικός Κβαντικός Αριθμός[]
- Ο Μαγνητικός Κβαντικός Αριθμός (ml = -l, -l+1, ... 0 ... ,l-1 ,l) είναι η ιδιοτιμή .
Ο αριθμός αυτός δίνει την τιμή της προβολής της τροχιακής στροφορμής, σε ένα συγκεκριμένο άξονα.
Σπινικός Κβαντικός Αριθμός[]
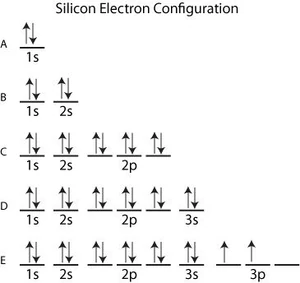
Πειραματικά αποτελέσματα, κυρίως από τη φασματοσκοπία, είχαν δείξει ότι μόνο μέχρι δύο ηλεκτρόνια μπορούν να βρίσκονται στην ίδια τροχιά.
Ο Pouli εισήγαγε τότε την περίφημη Απαγορευτική Αρχή Pouli, η οποία πήρε και το όνομά του, ώστε να συγκλίνει η θεωρία με τα πειραματικά αποτελέσματα.
Η εισαγωγή της απαγορευτικής αρχής, σύμφωνα με την οποία δύο ηλεκτρόνια δεν μπορούν να βρίσκονται στην ίδια κβαντική κατάσταση, απαιτούσε την εισαγωγή ενός τέταρτου κβαντικού αριθμού, άγνωστου έως τότε.
Η νέα ιδιότητα του ηλεκτρονίου, στην οποία αντιστοιχούσε ο νέος κβαντικός αριθμός, ονομάστηκε "κβαντική Ιδιοστροφορμή (spin), και η φυσική της σημασία δεν αναγνωρίστηκε αμέσως.
Αργότερα μόνο, κατανοήθηκε πως πρόκειται για μια εσωτερική ιδιότητα την οποία έχουν όλα τα σωματίδια και η οποία δεν έχει ανάλογο στην Κλασσική Φυσική.
Έχουμε λοιπόν τον τέταρτο κβαντικό αριθμό, ο οποίος είναι:
Ο Σπινικός Κβαντικός Αριθμός (m_s = -1/2 ή +1/2), η ιδιοστροφορμή του ηλεκτρονίου. Ο αριθμός αυτός δίνει την προβολή της κβαντικής ιδιοστροφορμής s = 1/2, στον συγκεκριμένο άξονα.
Σύνοψη Κβαντικών Αριθμών[]
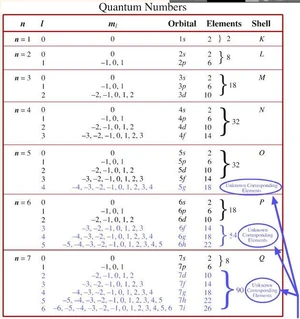
Για να συνοψίσουμε, η κβαντική κατάσταση ενός ηλεκτρονίου προσδιορίζεται από τους κβαντικούς αριθμούς:
| όνομα | σύμβολο | τροχιακό νόημα | πεδίο τιμών | παράδειγμα τιμής |
|---|---|---|---|---|
| Κύριος Κβαντικός Αριθμός | φλοιός | |||
| Αζιμουθιακός Κβαντικός Αριθμός (στροφορμή) | υποφλοιός | γισ : | ||
| Μαγνητικός Κβαντικός Αριθμός, (προβολή της στροφορμής) | μετατόπιση ενέργειας | για : | ||
| Σπινικός Κβαντικός Αριθμός | ιδιοστροφορμή (spin) | πάντα μόνο: |
Κβαντικοί αριθμοί με αλληλεπίδραση spin-τροχιάς[]
Όταν κάποιος λάβει υπ' όψιν του την αλληλεπίδραση ιδιοστροφορμής και τροχιάς, οι l, m και s δεν μετατίθενται πλέον με τη Χαμιλτονιανή, και η τιμή τους αλλάζει με την πάροδο του χρόνου. Οπότε, πρέπει να χρησιμοποιηθεί ένα νέο σύνολο κβαντικών αριθμών. Αυτό το σύνολο περιλαμβάνει:
- Τον κβαντικό αριθμό της ολικής στροφορμής (j = 1/2,3/2 ... n−1/2), ο οποίος δίνει την ολική στροφορμή μέσω της σχέσης , όπου h είναι η σταθερά Planck.
- Την προβολή της ολικής στροφορμής σε ένα άξονα (mj = -j,-j+1... j), που είναι ανάλογη με τον κβαντικό αριθμό m, και ικανοποιεί τη σχέση .
- Την Αρτιότητα. Αυτή είναι η ιδιοτιμή κάτω από αντιστροφή των αξόνων, και είναι θετική (+1) για καταστάσεις που προέρχονται από περιττά l και αρνητική (-1) για καταστάσεις που προέρχονται από άρτια l.
Παράδειγμα[]
Για παράδειγμα, έστω ότι έχουμε τις ακόλουθες οκτώ καταστάσεις, που ορίζονται από τους κβαντικούς αριθμούς:
- (1) l = 1, ml = 1, ms = +1/2
- (2) l = 1, ml = 1, ms = -1/2
- (3) l = 1, ml = 0, ms = +1/2
- (4) l = 1, ml = 0, ms = -1/2
- (5) l = 1, ml = -1, ms = +1/2
- (6) l = 1, ml = -1, ms = -1/2
- (7) l = 0, ml = 0, ms = +1/2
- (8) l = 0, ml = 0, ms = -1/2
Η κβαντική κατάσταση του συστήματος μπορεί να περιγραφεί ως Γραμμικός Συνδυασμός αυτών των οκτώ καταστάσεων.
Όμως, παρουσία της αλληλεπίδρασης spin-τροχιάς, εάν θέλει κάποιος να περιγράψει το ίδιο σύστημα με οκτώ καταστάσεις που είναι ιδιοδιανύσματα της Χαμιλτονιανής, θα έπρεπε να πάρει τις παρακάτω οκτώ καταστάσεις:
- j = 3/2, mj = 3/2, άρτια αρτιότητα (προέρχεται από την κατάσταση (1))
- j = 3/2, mj = 1/2, άρτια αρτιότητα (προέρχεται από τις καταστάσεις (2) και (3))
- j = 3/2, mj = -1/2, άρτια αρτιότητα (προέρχεται από τις καταστάσεις (4) και (5))
- j = 3/2, mj = -3/2, άρτια αρτιότητα (προέρχεται από την κατάσταση (6))
- j = 1/2, mj = 1/2, άρτια αρτιότητα (προέρχεται από τις καταστάσεις (2) και (3))
- j = 1/2, mj = -1/2, άρτια αρτιότητα (προέρχεται από τις καταστάσεις (4) και (5))
- j = 1/2, mj = 1/2, περιττή αρτιότητα (προέρχεται από την κατάσταση (7))
- j = 1/2, mj = -1/2, περιττή αρτιότητα (προέρχεται από την κατάσταση (8))
Άλλοι Κβαντικοί Αριθμοί[]
Τα στοιχειώδη σωματίδια περιέχουν αρκετούς εσωτερικούς κβαντικούς αριθμούς. Όμως, πρέπει να γίνει κατανοητό ότι τα στοιχειώδη σωματίδια είναι κβαντικές καταστάσεις του καθιερωμένου μοντέλου της Σωματιδιακής Φυσικής, οπότε οι κβαντικοί αριθμοί αυτών των σωματιδίων υπακούουν στην ίδια σχέση με την Χαμιλτονιανή αυτού του μοντέλου, όπως οι κβαντικοί αριθμοί του Πρότυπου Bohr για τη αντίστοιχη Χαμιλτονιανή του.
Με άλλα λόγια, κάθε κβαντικός αριθμός αντικατοπτρίζει και μια συμμετρία του προβλήματος.
Τυπικοί κβαντικοί αριθμοί που σχετίζονται με συμμετρίες του χωροχρόνου είναι
- η ιδιοστροφορμή (spin) (που σχετίζεται με τη συμμετρία στροφής),
- η αρτιότητα,
- η C-αρτιότητα και
- η Τ-αρτιότητα (που σχετίζεται με τη συμμετρία Poincare του χωροχρόνου).
Τυπικές εσωτερικές συμμετρίες είναι:
- οι λεπτονικοί αριθμοί
- οι βαρυονικοί αριθμοί
- το Ηλεκτρικό Φορτίο.
Ημικβαντικός Ταλαντωτής[]
Σύστημα ελατηρίου-σφαιριδίου (με μάζα (m)) εκτελεί ταλαντώσεις συχνότητας (f) και πλάτους (A)
Να βρεθεί ο Κβαντικός Αριθμός (n)
Η Ενέργεια (E) του Ταλαντούμενου Συστήματος είναι:
Αλλά
η Ενέργεια εκπεμπόμενης Θερμικής Ακτινοβολίας είναι:
Οπότε:
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
- Κβαντική Μηχανική
- Κυματοσυνάρτηση
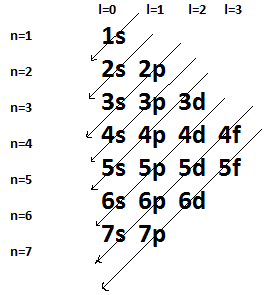
- Διαγώνιος Κανόνας
Βιβλιογραφία[]
Ατομική Φυσική[]
- Quantum Numbers and Electron Configurations
- Quantum numbers for the hydrogen atom
- Lecture notes on quantum numbers
Σωματιδιακή Φυσική[]
- David J., Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, 2004, id=ISBN 0-13-805326-X
- Halzen, Francis and Martin, Alan D., QUARKS AND LEPTONS: An Introductory Course in Modern Particle Physics, John Wiley & Sons,1984, ISBN 0-471-88741-2,
- The particle data group
Ιστογραφία[]
- Ομώνυμο άρθρο στην Βικιπαίδεια
- Αριθμός Ομώνυμο άρθρο στην Livepedia
- Ημικβαντικός Ταλαντωτής, Δρης
- lumenlearning.com
- quantum-numbers
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)




















