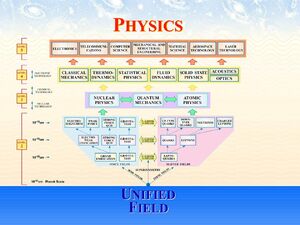
Κλασσική Σχετικότητα

Κλασσική Σχετικότης

Galilean relativity

Φυσική

Φυσική

---

Φυσικοί Γης
Νόμοι Φυσικής
Νόμοι Φυσικής
Θεωρίες Φυσικής
Πειράματα Φυσικής
Παράδοξα Φυσικής
Προβλήματα Φυσικής

Αδρανειακό Σύστημα Αναφοράς

Τραίνο
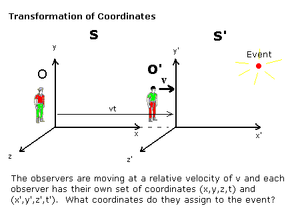
Σχετική Κίνηση

---

The velocity of the passenger
relative to the ground-based observer is vPG.
It is the vector sum of the velocity vPT
of the passenger relative to the train and
the velocity vTG of the train relative to
the ground:vPG = vPT + vTG.

- Ο βασικός τύπος της Σχετικότητας που χρησιμοποιείται στην Κλασσική Φυσική.

Ετυμολογία

Η ονομασία "Κλασσική" σχετίζεται ετυμολογικά με την λέξη "κλάση".

Εισαγωγή

Στηρίζεται στο δόγμα της ανυπαρξίας "απόλυτου κριτηρίου ακινησίας" οπότε δεν υπάρχει δυνατότητα να αποφανθεί ένας Παρατηρητής αν ένα σώμα είναι ακίνητο ή κινείται.

Σύμφωνα με αυτό η Κινητική Κατάσταση ενός σώματος μπορεί να καθορισθεί μόνον σχετικά δηλ. με αναφορά σε ένα ένα άλλο σώμα που αυθαίρετα θα θεωρηθεί "ακίνητο".

Ανάλυση

Η Κλασσική Σχετικότητα στηρίζεται στην ισοδυναμία (equivalence) όλων των αδρανειακών συστημάτων αναφοράς (inertial reference frames).

Βασική σημασία έχουν οι επιπρόσθετες θεωρήσεις του απόλυτου Χώρου (absolute space) και του απόλυτου Χρόνου (absolute time).

Με βάση τα ανωτέρω οι συντεταγμένες (coordinates) της θέσης ενός γεγονότος (event) (δηλ. ενός "σημείου" (point) στον Χώρο και στον Χρόνο)) περιγράφεται από δύο αδρανειακά συστήματα αναφοράς (inertial reference frames) που σχετίζονται μεταξύ τους με έναν Γαλιλαϊκό Μετασχηματισμό (Galilean transformation).

$\mathbf{r}^{\prime} = \mathbf{r} - \mathbf{r}_{0} - \mathbf{v} t$

$t^{\prime} = t - t_{0}$

όπου

$\mathbf{r}_{0}$ and $t_0$ είναι οι μετατοπίσεις από την αρχή του Χώρου και του Χρόνου,

$\mathbf{v}$ είναι η σχετική ταχύτητα (relative velocity) μεταξύ των δύο συστημάτων (inertial reference frames).

Ας σημειωθεί ότι υπό έναν Γαλιλαϊκό Μετασχηματισμό (Galilean transformation):

• the time between two events ($t_{2} - t_{1}$) is the same for all inertial reference frames and
• the distance between two simultaneous events (or, equivalently, the length of any object, $\left| \mathbf{r}_{2} - \mathbf{r}_{1} \right|$) is also the same.

Φυσικά Μεγέθη Κίνησης

Αδρανειακό Σύστημα Αναφοράς (Ορατό σε μεγέθυνση.

Τα δύο βασικά αξιώματα της Κλασσικής Σχετικότητας είναι:

1. There exists an Απόλυτος Χώρος (absolute space), in which Newton's laws are true. An inertial frame is a reference frame in relative uniform motion to absolute space.
2. All inertial frames share a Παγκόσμιος Χρόνος (universal time).

Consider two inertial frames S and S' .

A physical event in S will have position coordinates r = (x, y, z) and time t; similarly for S' .

By the second axiom above, one can synchronize the clock in the two frames and assume t = t' .

Suppose S' is in relative uniform motion to S with velocity v.

Consider a point object whose position is given by r = r(t) in S.

We see that

$r'(t) = r(t) - v t.\,$

The velocity of the particle is given by the time derivative of the position:

$u'(t) = \frac{d}{d t} r'(t) = \frac{d}{d t} r(t) - v = u(t) - v.$

Another differentiation gives the acceleration in the two frames:

$a'(t) = \frac{d}{d t} u'(t) = \frac{d}{d t} u(t) - 0 = a(t).$

Εσωτερική Αρθρογραφία

• Κλασσική Μηχανική
• Γαλιλαϊκός Μετασχηματισμός
• Σχετική Κίνηση
• Προκλασσική Σχετικότητα
• Αριστοτέλεια Μηχανική
• Ειδική Σχετικότητα
• Γενική Σχετικότητα

Βιβλιογραφία

• Πανεπιστήμιο Πατρών]
• Μηχανική Παντίκου

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---