Κυματοσυνάρτησις




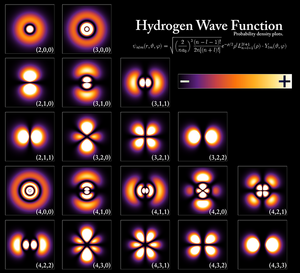
υδρογόνου
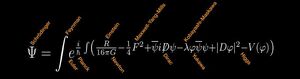
Μερικοί νομίζουν ότι η Επιστήμη
δημιουργείται από φαεινές ρηξικέλευθες ιδέες
κάποιων φωτισμένων ανθρώπων
που αποκαλούν "ευφυίες"
Όμως, η Αλήθεια είναι πολύ διαφορετική.
Η Επιστήμη κτίζεται πέτρα-πέτρα
από δεκάδες χιλιάδες "μέτριους" ανθρώπους
που απλά μόχθησαν αρκετά
για να κατανοήσουν τα σκαλοπάτια
που πρόσθεσαν οι προηγούμενοι.
Καλό παράδειγμα
η σύγχρονη εξίσωση της Κυματοσυνάρτησης.
Διάφοροι φυσικοί συνεισέφεραν κατά καιρούς
το μερίδιό τους
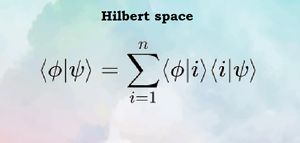
Χώρος Hilbert
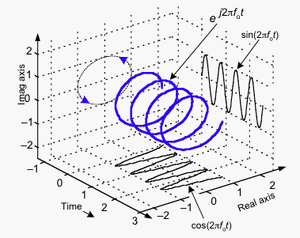
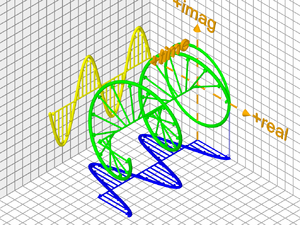
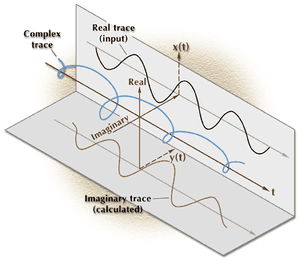
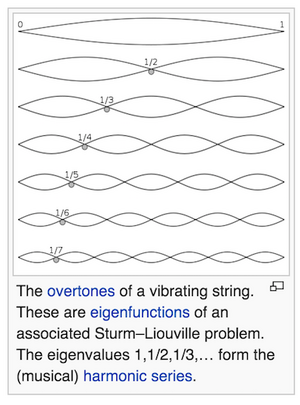
Δονούμενη Χορδή
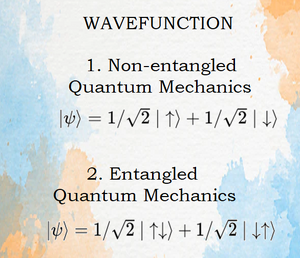
Κυματοσυνάρτηση
- Μία μιγαδική συνάρτηση που έχει κεντρικό ρόλο στην Κβαντική Φυσική.
Ετυμολογία[]
Το όνομα "Κβαντική" σχετίζεται ετυμολογικά με την λέξη "κβάντο".
Εισαγωγή[]
Στην περίπτωση των μηχανικών κυμάτων η κυματοσυνάρτηση ψ είναι ένα κλασσικό Φυσικό Μέγεθος όπως π.χ. η απόσταση των μορίων μιας χορδής από τη θέση ισορροπίας τους, η ένταση του Ηλεκτρικού Πεδίου και η ένταση του Μαγνητικού Πεδίου στα Ηλεκτρομαγνητικά Κύματα.
Στην περίπτωση των σωματιδίων που συμπεριφέρονται ως κύματα De Broglie δεν πρέπει να θεωρήσουμε ότι τα σωματίδια καταλαμβάνουν έκταση όση και το κυματόδεμα ή ότι η κυματοσυνάρτηση εκφράζει την κατανομή της μάζας τους στο χώρο. Η αντίληψη αυτή είναι λανθασμένη.
Όταν αποδείχθηκε η ορθότητα της εξίσωσης Schrödinger, κατέστη η δημοφιλέστερη ανάμεσα στους επιστημονικούς κύκλους. Αργότερα, όμως, άνοιξε η συζήτηση για την φύση της κυματοσυνάρτησης ψ και ως προς αυτό το ζήτημα οι φυσικοί διαιρέθηκαν σε δύο στρατόπεδα.
Πάντως η υιοθέτηση της μιγαδικής κυματοσυνάρτησης σηματοδοτεί την μη-Απομονωσιμότητα του παρατηρούμενου Αντικειμένου από το Περιβάλλον του (έμμεσο ή άμεσο)
Ημικλασσική Ερμηνεία[]
Στην πρώτη ομάδα των επιστημόνων, ο Schrödinger απέδιδε φυσική σημασία στην κυματοσυνάρτηση.
Όπου:
- M = ο Φυσικός Χώρος (που αντιπροσωπεύεται από ένα Λείο Πολύπτυχο)
- V = o Χώρος Hilbert
Το κβαντικό άλμα που συντελούταν στο άτομο κατά τη μετάβασή του από τη μια κατάσταση στην άλλη ερμηνευόταν ως μετασχηματισμός, που οδηγούσε το σύστημα από την κατάσταση που αντιστοιχεί σε ταλαντώσεις με ενέργεια Εm στην κατάσταση με ενέργεια Εn, ενώ η πλεονάζουσα ενέργεια ακτινοβολείται ως Ηλεκτρομαγνητικό Κύμα.
Το ηλεκτρόνιο θεωρήθηκε ως ένα φορτισμένο νέφος που περιέβαλλε τον πυρήνα του ατόμου και μπορούσε να παρουσιάζει ενεργειακές μεταπτώσεις παράγοντας ένα χωρικά κατανεμημένο Ηλεκτρομαγνητικό Κύμα το οποίο διαδίδεται με συνεχή τρόπο χωρίς κβαντικά άλματα.
Έτσι συνυπήρχε αρμονικά η Κβαντική με την Κλασσική Φυσική. Την άποψη αυτή ασπάστηκαν οι Louis De Broglie, Albert Einstein, o Max von Laue και o Max Planck.
Κυματοσωματιδιακή Ερμηνεία[]
Η δεύτερη ομάδα, που περιλάμβανε τους Wolfgang Pauli, Werner Heisenberg και Niels Bohr, θεωρούσε ότι η ημικλασσική ερμηνεία της κυματομηχανικής ήταν εσφαλμένη και ότι αποκλειόταν να κατασκευαστεί μια συνεπής Κβαντική Θεωρία χωρίς την έννοια του κυματοσωματιδιακού δυϊσμού.
Πιθανοκρατική Ερμηνεία[]
Όμως, αργότερα ο Max Born, το 1926, με πειράματα σκέδασης των ηλεκτρονίων και των σωματίων άλφα από πυρήνες, πρόσφερε την κλείδα της κατανόησης για την φυσική ερμηνεία της κυματοσυνάρτησης (ψ).
Το τετράγωνο της πρέπει να εκληφθεί ως η πιθανότητα να βρεθεί το σωματίδιο σε ένα δεδομένο σημείο του Χώρου περί τον πυρήνα ή η πυκνότητα του ηλεκτρονιακού νέφους γύρω από τον πυρήνα. Κατά συνέπεια η κυματοσυνάρτηση περιγράφει μεμονωμένα συμβάντα (όπως η εκπομπή ενός κβάντου φωτός) μόνο κατά το ότι καθορίζει την πιθανότητα πραγματοποίησης τους. Αυτή η ερμηνεία προσέφερε επιτέλους μία σταθερή βάση στην Κβαντική Φυσική.
Καταστατικό Διάνυσμα[]
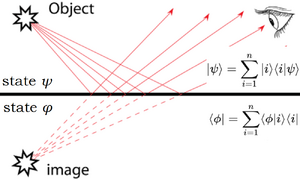
Συμβολισμός Dirac
- where:
Είναι αντίστοιχο με το σύνηθες
- where:
Επίσης
Αν ψ είναι η αρχική κατάσταση ενός κβαντικού συστήματος
και φ είναι μία τελική κατάστασή του
και i είναι οι ιδιοκαταστάσεις του συστήματος ως προς κάποιο φυσικό μέγεθος
τότε:
Η αντιστοιχία με το εσωτερικό γινόμενο στο φυσικό Ευκλείδειο Χώρο είναι:
Η αντίδραση του Einstein[]
Ο Einstein αντιδρώντας στην πιθανοκρατική ερμηνεία της σχολής της Κοπεγχάγης που εισήγαγε ο Max Born, του έγραψε μια επιστολή που έμεινε στην ιστορία της Φυσικής:
Πιστεύετε σε ένα Θεό που παίζει ζάρια, ενώ εγώ στην πλήρη τάξη και νομοτέλεια του αντικειμενικού Κόσμου. Ακόμη και η αρχική μεγάλη επιτυχία της Κβαντικής Θεωρίας δεν με κάνει να πιστεύω σε έναν πιθανοκρατικό Κόσμο, αν και γνωρίζω καλά, ότι οι νεώτεροι συνάδελφοί σου αποδίδουν την εμμονή μου σε γεροντική άνοια.
Σήμερα η πιθανοκρατική ερμηνεία της κυματοσυνάρτησης έχει επικρατήσει πλήρως.
Ανάλυση[]
H κυματοσυνάρτηση (η οποία συνήθως συμβολίζεται με το ελληνικό γράμμα ) είναι η συνάρτηση που ικανοποιεί την εξίσωση Schrödinger της Κβαντικής Μηχανικής και στην ουσία περιγράφει ένα κύμα.
Σε αυτήν περιέχεται η πληροφορία για την κίνηση ενός σωματίου στο Χώρο, αφού βάσει της θεώρησης του De Broglie που επιβεβαιώθηκε και πειραματικά, ένα σωμάτιο συμπεριφέρεται ως ένα κύμα με μήκος κύματος:
όπου h η σταθερά δράσεως του Planck και p το μέτρο της ορμής του. Ισοδύναμα, η παραπάνω σχέση μπορεί να εκφρασθεί συναρτήσει του κυματαριθμού (k) και της ανηγμένης σταθεράς του Planck (ħ) ως εξής:
Όταν αυτό το μήκος κύματος που φέρει το όνομα μήκος De Broglie είναι συγκρίσιμο με τις διαστάσεις του Χώρου στον οποίο βρίσκεται, τότε εκδηλώνονται οι κυματικές ιδιότητες των σωμάτων.
Παρόλο που στην κυματοσυνάρτηση εμπεριέχεται όλη η γνωστή πληροφορία ενός συστήματος, στην ίδια δεν αποδίδεται φυσικό νόημα ή περιεχόμενο.
Σύμφωνα με τη στατιστική ερμηνεία που πρωτοδιατυπώθηκε από τον Max Born το 1926, το τετράγωνο του μέτρου της κυματοσυνάρτησης είναι αυτό που έχει φυσικό νόημα, καθώς αποτελεί την πυκνότητα πιθανότητας των φυσικών μεγεθών.
Σύμφωνα με τη στατιστική ερμηνεία του Born, η ποσότητα |Ψ(r)|² δίνει την πυκνότητα πιθανότητας να βρεθεί ένα σωματίδιο που περιγράφεται από τη κυματοσυνάρτηση αυτή μέσα σε ένα στοιχειώδες όγκο d³r γύρω από τη θέση r.
In order to define the oscillations completely one additional quantity must be known: the phase (φ).
The phase (φ) measures the displacement of the wave from some arbitrary reference point and is usually expressed as an angle.
If at some point the real part of the κυματοσυνάρτησης of the electron but instead oscillation, say, has its maximum positive amplitude, the phase (φ) at that point might be assigned the value zero degrees.
Where the real part next falls to zero the phase (φ) is 90 degrees and where it reaches its negative maximum the phase (φ) is 180 degrees. In general the imaginary part of the amplitude, is 90 degrees out of phase with the real part, so that whenever one part has a maximal value the other part is zero.
It is apparent that the only way to determine the phase (φ) of an Electron κυματοσυνάρτησης is to disentangle the contributions of the real and the imaginary parts of the amplitude. That turns out to be impossible, even in principle.
The sum of the squares of the real and the imaginary parts can be known, but there is no way of telling at any given point or at any moment how much of the total derives from the real part and how much from the imaginary part.
Indeed, an exact symmetry of the theory implies that the two contributions are indistinguishable. Differences in the phase (Δφ) of the field at two points or at two moments can be measured, but not the absolute phase (φ).
The finding that the phase (φ) of an electron wave is inaccessible to measurement has a corollary : the phase (φ) cannot have an influence on the outcome of any possible experiment.
If it did, that experiment could be used to determine the phase (φ). Hence the electron κυματοσυνάρτηση exhibits a symmetry with respect to arbitrary changes of phase (φ). Any phase angle (φ) can be added to or subtracted from the electron κυματοσυνάρτηση and the results of all experiments will remain invariant.
Φάση Κυματοσυνάρτησης[]
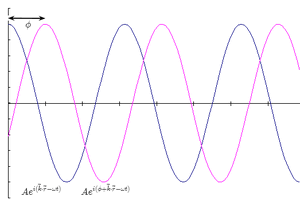
this graph shows the real part of
- Ψ(r, t, φ1) in blue
- Ψ(r, t, φ2) in purple
Obviously Ψ is a function of two variables
so you can regard the graph either as
- keeping space (r) constant and varying time (t)
- keeping time (t) constant and varying space (r)
The quantity ϕ is just the phase difference
between the two waves
e.g. the distance between the peaks shown by the arrow on the diagram.
The absolute value of ϕ has no physical significance because you can measure ϕ from any reference point you want. However the difference in ϕ between two wavefunctions has a very important physical meaning because it determines how the waves will interfere.
Συνθήκη Κανονικοποίησης[]
Επειδή είναι βέβαιο γεγονός ότι ένα σωμάτιο αναγκαστικά θα υπάρχει σε κάποια θέση στο Χώρο, θα πρέπει η συνολική πιθανότητα να βρούμε το σωματίδιο σε ολόκληρο το Χώρο να ισούται με μονάδα.
Μαθηματικά, αυτό μεταφράζεται στην απαίτηση
όπου η ολοκλήρωση γίνεται σε ολόκληρο το χώρο.
Έτσι, αν το ολοκλήρωμα μίας κυματοσυνάρτησης είναι πεπερασμένο (δεν απειρίζεται, ή αυστηρότερα είναι τετραγωνικά ολοκληρώσιμη) και ίσο με τη μονάδα με μία σταθερά Μ≠1, αρκεί για να βρούμε την κυματοσυνάρτηση ενός συστήματος να διαιρέσουμε την κυματοσυνάρτηση αυτή με Μ.
Δηλαδή αν
- τότε:
- όπου ΨM η μη κανονικοποιημένη κυματοσυνάρτηση.
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
- Κατάρρευση Κυματοσυνάρτησης
- Κυματοσυνάρτηση spin
- Βαθμιδική Θεωρία
- Κβαντική Μηχανική
- Κβαντική Κατάσταση
- Επίπεδο Κύμα
- Συμβολισμός Dirac
Βιβλιογραφία[]
- Τραχανάς Στέφανος, Κβαντομηχανική Ι, Πανεπιστημιακές Εκδόσεις Κρήτης (2009)
- Τραχανάς Στέφανος, Κβαντομηχανική ΙΙ, Πανεπιστημιακές Εκδόσεις Κρήτης (2009)
- Ταμβάκης Κυριάκος, Εισαγωγή στην Κβαντομηχανική, Leader Books 2003
Ιστογραφία[]
- Ομώνυμο άρθρο στην Βικιπαίδεια
- Ομώνυμο άρθρο στην Livepedia
- physics4u.gr
- what-is-phase-angle-of-wave-function
- Alain Aspect: ο άνθρωπος που απέδειξε πειραματικά ότι ο Θεός παίζει ζάρια
- Spin wave functions
- science4all.org
- Hilbert space vs. Projective Hilbert space
- Topology in nonrelativistic quantum mechanics
- Κυματοσυνάρτηση
- videoclip
- video
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)


















