Ακολουθία
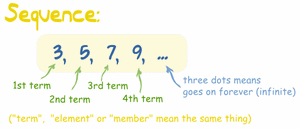


Σειρά
Μαθηματική Σύγκλιση

Μαθηματική Σύγκλιση
Μαθηματική Σύγκλιση
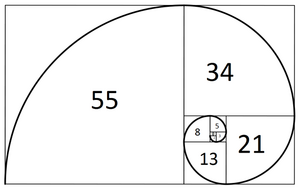
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...

Μαθηματικό Όριο
- Ένα Μαθηματικό Δόμημα
Ετυμολογία[]
Η ονομασία "Ακολουθία" σχετίζεται ετυμολογικά με την λέξη "[[ ]]".
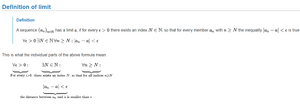
Ορισμός[]
Ακολουθία (πραγματικών αριθμών) ονομάζεται κάθε συνάρτηση που το "σύνολο ορισμού" της είναι το σύνολο των φυσικών αριθμών (Ν), ή ένα υποσύνολο του (πεπερασμένο ή άπειρο) (σύνολο αφίξεως).
Όλες οι ακολουθίες ως συναρτήσεις είναι σύνολα διατεταγμένων ζευγών. Παρόλα αυτά μια πεπερασμένη ακολουθία μπορούμε να την αντιμετωπίζουμε ως διατεταγμένη n-άδα για ευκολία και επομένως μπορούμε να τη συμβολίσουμε με .
Παρομοίως, για μια άπειρη ακολουθία μπορούμε να χρησιμοποιούμε το συμβολισμό όπου είναι ο πρώτος όρος της, ο δεύτερος κ.ο.κ.
Επίσης μια άπειρη ακολουθία συμβολίζεται και ως , ή για συντομία .
Εισαγωγή[]
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters.
Like a set, it contains members (also called elements, or terms). The number of elements (possibly infinite) is called the length of the sequence.
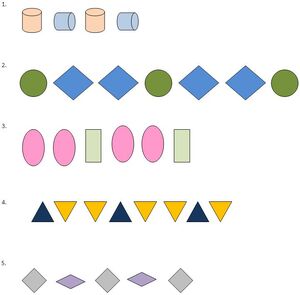
Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
Επομένως, ακολουθία είναι μια ειδική μορφή συνάρτησης, συνεπώς υπάρχουν:
- φράγματα ακολουθίας,
- μονοτονία ακολουθίας,
- ακρότατα ακολουθίας,
- γραφική παράσταση ακολουθίας κ.λ.π.
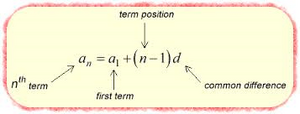
Ειδική κατηγορία ακολουθιών είναι και οι πρόοδοι:
Ανάλυση[]
Ονομάζουμε ακολουθία ή πιο συγκεκριμένα άπειρη ακολουθία οποιαδήποτε συνάρτηση α από το σύνολο των φυσικών σε ένα σύνολο Α, δηλαδή κάθε συνάρτηση:
Ονομάζουμε πεπερασμένη ακολουθία ή λίστα ν στοιχείων οποιαδήποτε συνάρτηση α από ένα σύνολο των φυσικών σε ένα σύνολο Α, δηλαδή κάθε συνάρτηση:
όπου το σύνολο ορίζεται ως .
Συνηθίζεται να συμβολίζουμε μια ακολουθία με:
ή με
και μια πεπερασμένη ακολουθία με τα σύμβολα:
ή με
- .
Επίσης συνηθίζεται να συμβολίζουμε την τιμή μιας ακολουθίας, για κάθε στοιχείο ή αντίστοιχα, με αντί με όπως συνηθίζεται γενικά για τις συναρτήσεις.
Διευκρινίζεται ότι αν το σύνολο Α είναι ίσο με το σύνολο των πραγματικών αριθμών τότε η ακολουθία ονομάζεται πραγματική ακολουθία.
Όλες οι ακολουθίες ως συναρτήσεις είναι σύνολα διατεταγμένων ζευγών.
Ωστόσο μια πεπερασμένη ακολουθία μπορούμε να την αντιμετωπίζουμε ως διατεταγμένη ν-άδα για ευκολία και επομένως μπορούμε να τη συμβολίσουμε με
- .
Παρόμοια, για μια άπειρη ακολουθία μπορούμε να χρησιμοποιούμε το συμβολισμό
- .
΄
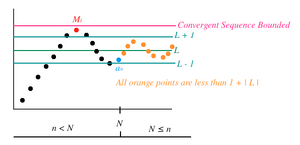
Σύγκλιση Ακολουθίας[]
Μία ακολουθία είναι συγκλίνουσα (ή αλλιώς συγκλίνει στο όριο l) όταν:
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
Βιβλιογραφία[]
Ιστογραφία[]
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

























