Ομάδα Lie

Ομάδα Lie

Lie Group

Ομάδα Lie

Ομάδα Lie

Ομάδα Lie
Ομάδα E8

Ομάδα Lie

Ομάδα Lie

Ομάδα Lie
Άλγεβρα Lie

Ομαδοθεωρία
Αλγεβρική Ομάδα

---

Γενική Γραμμική Ομάδα
Ορθογώνια Ομάδα
Μοναδιακή Ομάδα
Μαθηματική Αναπαράσταση
Μαθηματική Μήτρα

Ομάδα Lie
Άλγεβρα Lie

Ομαδιαία Δράση
Μαθηματικό Πολύπτυχο
Ομάδα Lie
Άλγεβρα Lie

- Μία Ομάδα.

Ετυμολογία

Η ονομασία "ομάδα" σχετίζεται ετυμολογικά με την λέξη '"ομού".

Η ονομασία "Ομάδα Lie " σχετίζεται ετυμολογικά με το όνομα "Lie". They are named after the nineteenth century Norwegian mathematician Sophus Lie, who laid the foundations of the theory of continuous transformation groups.

Εισαγωγή

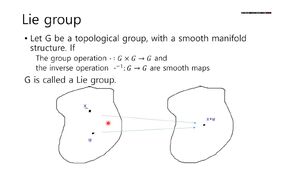
Μία Ομάδα Lie είναι μία Μαθηματική Ομάδα (group) που επίσης είναι διαφορίσιμο Πολύπτυχο (differentiable manifold), εφοδιασμένο με την ιδιότητα ότι οι group operations είναι συμβατές με την smooth structure.

Μια ομάδα Lie G, επίσης, είναι ένα λείο Πολύπτυχο με δομή ομάδας, τέτοιο ώστε οι πράξεις του πολλαπλασιασμού και αντιστροφής να είναι διαφορίσιμες.

Βασικό χαρακτηριστικό των ομάδων Lie είναι ότι η γεωμετρία τους παραμένει αναλλοίωτη σε όλα τα σημεία τους.

Οπότε, η μελέτη της γεωμετρίας μιας ομάδας Lie G ανάγεται στη μελέτη της γεωμετρίας σε μια περιοχή του ουδετέρου στοιχείου της e και συγκεκριμένα, στη μελέτη της άλγεβρας Lie της G, δηλαδή τον εφαπτόμενο διανυσματικό χώρο της G στο e.

Παραδείγματα

Από τα Μαθηματικά και την Φυσική:

• Ευκλείδειος Χώρος (Euclidean space) Rⁿ είναι μία abelian Lie ομάδα (with ordinary vector addition as the group operation).
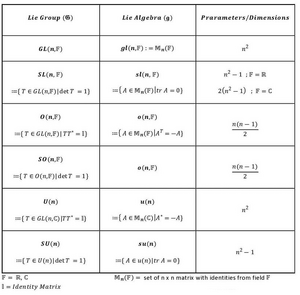
• The group GL_n(R) of invertible matrices (under matrix multiplication) is a Lie group of dimension n², called the Γενική Γραμμική Ομάδα (general linear group). It has a subgroup SL_n(R) of matrices of determinant 1 which is also a Lie group, called the Ειδική Γραμμική Ομάδα (special linear group).
• The Ορθογώνια Ομάδα (orthogonal group) O_n(R) είναι μία Lie ομάδα represented by Ορθογώνιες μήτρες (orthogonal matrices). It consists of all στροφές (rotations) and αντιστροφές (improper rotations or reflections) of an n-dimensional vector space. It has a subgroup SO_n(R) of elements of determinant 1, called the Ειδική Ορθογώνια Ομάδα (special orthogonal group) or Στροφική Ομάδα (rotation group).
• The Μοναδιακή Ομάδα (unitary group) U(n) is a compact group of dimension n² represented by Μοναδιακές μήτρες (unitary matrices). It has a subgroup SU(n) of elements of determinant 1, called the Ειδική Μοναδιακή Ομάδα (special unitary group).
• Spin groups are double covers of the special orthogonal groups, used for studying φερμιόνια (fermions) in Κβαντική Πεδιακή Θεωρία (quantum field theory) (among other things).
• The group Sp_2n(R) of all matrices preserving a symplectic form is a Lie group called the Συμπλεκτική Ομάδα (symplectic group).
• The spheres S⁰, S¹, and S³ can be made into Lie groups by identifying them with the real numbers, complex numbers, or quaternions of absolute value 1 respectively. No other spheres are Lie groups. The Lie group S¹ is sometimes called the Κυκλική Ομάδα (circle group).
• The group of upper triangular n by n matrices is a solvable Lie group of dimension n(n + 1)/2.
• The Ομάδα Lorentz (Lorentz group) and the Ομάδα Poincare (Poincare group) of isometries of Χωρόχρονου (spacetime) are Lie groups of dimensions 6 and 10 that are used in Ειδική Σχετικότητα (special relativity).
• The Ομάδα Heisenberg (Heisenberg group) is a Lie group of dimension 3, used in Κβαντική Φυσική.
• The group U(1)×SU(2)×SU(3) is a Lie group of dimension 1+3+8=12 that is the Βαθμιδική Ομάδα (gauge group) of the Σωματιδιακό Καθιερωμένο Πρότυπο (standard model), whose dimension corresponds to the 1 φωτόνιο (photon) + 3 ασθενόνια (vector bosons) + 8 γλοιόνια (gluons) of the standard model.
• The Μεταπλεκτική Ομάδα (metaplectic group) is a 3 dimensional Lie group that is a double cover of SL₂(R) and is used in the theory of modular forms. It cannot be represented as finite matrices.
• The Εξαιρετικές Ομάδες (exceptional Lie groups) of types G₂, F₄, E₆, E₇, E₈ have dimensions 14, 52, 78, 133, and 248. There is also a group E_7½ of dimension 190.

For many more examples see the table of Lie groups and list of simple Lie groups and article on matrix groups.

Παραδείγματα ομάδων Lie είναι

• 1) Οι πραγματικοί αριθμοί εφοδιασμένοι με την πράξη της πρόσθεσης
• 2) U(n), μοναδιστικοί γραμμικοί μετασχηματισμοί του C^n
• 3) SU(n), μοναδιστικοί γραμμικοί μετασχηματισμοί του C^n με det = 1
• 4) O(n), ορθογώνιοι γραμμικοί μετασχηματισμοί του R^n
• 5) SO(n), ορθογώνιοι γραμμικοί μετασχηματισμοί του R^n με det = 1
• 6) GL(n), αντιστρέψιμοι γραμμικοί μετασχηματισμοί ενός διανυσματικού χώρου V.

There are several standard ways to form new Lie groups from old ones:

• The product of two Lie groups is a Lie group.
• Any closed subgroup of a Lie group is a Lie group.
• The quotient of a Lie group by a closed normal subgroup is a Lie group.
• The universal cover of a connected Lie group is a Lie group. For example, the group R is the universal cover of the circle group S¹.

Some examples of groups that are not Lie groups are:

• Infinite dimensional groups, such as the additive group of an infinite dimensional real vector space. These are not Lie groups as they are not finite dimensional manifolds.
• Some totally disconnected groups, such as the Galois group of an infinite extension of fields, or the additive group of the p-adic numbers. These are not Lie groups because their underlying spaces are not real manifolds. (Some of these groups are "p-adic Lie groups".)
• The image of a connected Lie group under a homomorphism of Lie groups need not be a Lie group. The usual example of this is the image of R in the group R²/Z² (≅ S¹×S¹) under the map x→(x,√2 x). The image is a dense subset of R²/Z² that is not a manifold, and so is not a Lie group. This also gives an example where a subalgebra of a Lie algebra does not correspond to a Lie subgroup of the corresponding Lie group.
• The group of rational numbers under addition, topologized as a subset of the real numbers, is not a Lie group as it is not a manifold.

Τύποι

Lie groups are classified according to their algebraic properties (Απλή Ομάδα (simple group), Ημιαπλή Ομάδα (semisimple group), solvable, nilpotent, Αβελιανή Ομάδα (abelian), their connectedness (connected or simply connected) and their compactness.

• The identity component of any Lie group is an open normal subgroup, and the Ομάδα Πηλίκου (quotient group) is a Διακριτή Ομάδα (discrete group).

• The universal cover of any connected Lie group is a simply connected Lie group, and conversely any connected Lie group is a quotient of a simply connected Lie group by a discrete normal subgroup of the center.

• Compact Lie groups are all known: they are finite central extensions of a product of copies of the circle group S¹ and simple compact Lie groups (which correspond to connected Dynkin diagrams).

• Any simply connected solvable Lie group is isomorphic to a closed subgroup of the group of invertible upper triangular matrices of some rank, and any finite dimensional irreducible representation of such a group is 1 dimensional. Solvable groups are too messy to classify except in a few small dimensions.

• Any simply connected nilpotent Lie group is isomorphic to a closed subgroup of the group of invertible upper triangular matrices with 1's on the diagonal of some rank, and any finite dimensional irreducible representation of such a group is 1 dimensional. Like solvable groups, nilpotent groups are too messy to classify except in a few small dimensions.

• Simple Lie groups are sometimes defined to be those that are simple as abstract groups, and sometimes defined to be connected Lie groups with a simple Lie algebra. For example, SL₂(R) is simple according to the second definition but not according to the first. They have all been classified (for either definition).

• Semisimple Lie groups are connected groups whose Lie algebra is a product of simple Lie algebras. They are central extensions of products of simple Lie groups.

• Connected abelian Lie groups are all isomorphic to products of copies of R and the circle group S¹.

Δομή

Any Lie group G can be decomposed into discrete, simple, and abelian groups in a canonical way as follows. Write

G_con for the connected component of the identity

G_sol for the largest connected normal solvable subgroup

G_nil for the largest connected normal nilpotent subgroup

so that we have a sequence of normal subgroups

1 ⊆ G_nil ⊆ G_sol ⊆ G_con ⊆ G

Then

G/G_con is discrete

G_con/G_sol is a central extension of a product of simple connected Lie groups.

G_sol/G_nil is abelian (and a product of copies of R and S¹)

G_nil/1 is nilpotent, and therefore its ascending central series has all quotients abelian.

This can be used to reduce some problems about Lie groups (such as finding their unitary representations) to the same problems for connected simple groups.

Ομάδες Lie και Φυσική

Οι ομάδες Lie κατέχουν ιδαίτερο ρόλο στην ανακάλυψη της Ενιαίας Θεωρίας Πεδίου, δηλαδή της θεωρίας που θα ενσωματώνει "με ομογενή τρόπο" τη Βαρυτική Φυσική (δηλ. την Γενική Σχετικότητα) και τη Σωματιδιακή Φυσική και επομένως θα ερμηνεύει σε βαθύτερο επίπεδο τους φυσικούς νόμους της ύλης.

Πρέπει να ειπωθεί εδώ ότι τα Μαθηματικά είναι η «γλώσσα» που στην οποία είναι "εκπεφρασμένοι" οι Φυσικοί Νόμοι που διέπουν την λειτουργία της Φύσης.

Η σημαντικότερη συμβολή των ομάδων Lie στην Φυσική αποκαλύφθηκε την δεκαετία του 1960 όταν ο Murray Gell-Mann ανακάλυψε ότι τα στοιχειώδη σωματίδια μπορούν να ομαδοποιηθούν με βάση τη μάζα, το φορτίο και άλλες ιδιότητές τους, έτσι ώστε να αποδοθούν από ομάδες Lie.

Μάλιστα, τοποθέτησε τα ως τότε γνωστά υποατομικά σωματίδια στο «χάρτη» της ομάδας SΟ(3), προβλέποντας ότι έπρεπε να βρεθεί και ένα ακόμη σωματίδιο, το $\Omega ^{-}$ που θα κάλυπτε τη θέση που έμενε κενή.

Τις δεκαετίες που ακολούθησαν αναπτύχθηκε το Καθιερωμένο Σωματιδιακό Πρότυπο, που χρησιμοποιεί μια σύνθεση τριών ομάδων Lie (τις U1, SU(2) και SU(3)) για να συσσωματώσει όλα τα γνωστά στοιχειώδη σωματίδια καθώς και τις τρεις από τις τέσσερις θεμελιώδεις φυσικές δυνάμεις (πεδία):

• τον ηλεκτρομαγνητισμό,
• την ισχυρή πυρηνική δύναμη που συγκρατεί τους πυρήνες για να μη διασπαστούν και
• την ασθενή πυρηνική δύναμη, που καθορίζει τα φαινόμενα της ραδιενέργειας.

Φαινόταν μόνο ζήτημα χρόνου να βρεθεί μια ακόμα ομάδα Lie, που θα μπορούσε να καλύψει τα πάντα, συμπεριλαμβανομένης της βαρύτητας.

Αλλά η Βαρύτητα, αποδείχθηκε "σκληρό καρύδι". Όλες οι προσπάθειες οδηγούσαν στην πρόβλεψη φαινομένων που δεν είχαν παρατηρηθεί στη Φύση, όπως η φυσική αποσύνθεση του πρωτονίου.

Τελικά, τη δεκαετία του 1980 άλλες θεωρίες ενοποίησης των πεδίων και των υποατομικών σωματιδίων, μεταξύ αυτών και η Θεωρία Χορδών, εκτόπισαν τη χρήση των ομάδων Lie.

Το 2007 ο Antony Garrett Lisi, παρουσιάζει τη δική του εκδοχή για τη «θεωρία των πάντων», χρησιμοποιώντας την πιο σύνθετη και κομψή ομάδα Lie, την Ομάδα E8. Ήταν ακριβώς η εργασία του αυτή που έδωσε νέα ώθηση για την ενοποίηση της βαρύτητας με το Καθιερωμένο Σωματιδιακό Πρότυπο.

Άλλοι προχώρησαν την ιδέα αυτή με διαφορετικό τρόπο. Αντί να θεωρήσουν τις ομάδες Lie ως «κυτία» που συγκρατούν δυνάμεις και σωματίδια, τα αναλύουν στα μαθηματικά δομικά τους στοιχεία: ένα αριθμητικό σύστημα οκτώ διαστάσεων, τα οκτόνια.

Πολλοί μαθηματικοί αποφεύγουν τα οκτόνια, επειδή δεν υπακούν στους τυπικούς κανόνες της άλγεβρας και δίνουν διαφορετικό αποτέλεσμα ανάλογα με τη σειρά που θα πραγματοποιηθούν οι μαθηματικές πράξεις.

Όμως, ο Tevian Dray και Corinne Manogue χρησιμοποίησαν ακριβώς αυτήν την ενοχλητική ασυμμετρία για να εξηγήσουν τις «ιδιοτροπίες» ορισμένων σωματιδίων, όπως των νετρίνων που είναι αποκλειστικά αριστερόστροφα ως προς το spin (μια από τις φυσικές ιδιότητες των υποατομικών σωματιδίων).

Τα οκτόνια είναι επίσης ιδιαίτερα κατάλληλα για την πραγματοποίηση υπολογισμών στις 10 διαστάσεις, τομέα δράσης των θεωρητικών των υπερχορδών, που υποστηρίζουν ότι το Σύμπαν πέραν από τις τέσσερις διαστάσεις (τρεις του χώρου και μια του χρόνου) έχει άλλες 6 που είναι «συσπειρωμένες» και για αυτό όχι παρατηρήσιμες από εμάς. Τα οκτόνια μπορούν να εξηγήσουν εύκολα την κατάρρευση των επιπλέον διαστάσεων.

Υπάρχουν όμως και πολλοί επιστήμονες που θεωρούν ότι βρίσκονται σε λάθος δρόμο όσοι αναζητούν ενοποιημένη θεωρία στη βάση των ομάδων Lie. Και αυτό διότι και οι νέες εκδοχές των θεωριών με ομάδες Lie προβλέπουν σωματίδια που αν υπήρχαν στη Φύση είναι σχεδόν βέβαιο ότι θα είχαν εντοπισθεί από πειράματα που έχουν ήδη γίνει.

Ο Lisi, που παρουσίασε το 2010 μια βελτιωμένη εκδοχή, της στηριγμένης στην ομάδα E8 θεωρίας του, παρατηρεί ότι αν τα υπεράριθμα σωματίδια που προβλέπονται έχουν πολύ μεγαλύτερο βάρος από τα συμμετρικά τους φερμιόνια, τότε είναι φυσικό να μην έχουν εντοπισθεί.

Άλγεβρα Lie

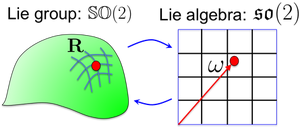
Every Lie Group has an associated Lie Algebra

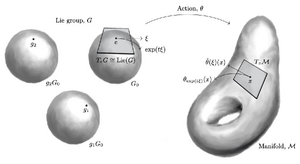
They are related via the exponential map

exp(Lie Algebra) = Lie Group

The Lie Algebra can be represented by a number of infinitesimal generators or matrices that generate the Lie Group

The number of matrices needed to generate a Lie Group is the same as the dimension of the group:

• SU(n) groups have dimension n2-1
• SO(n) groups have dimension n(n-1)/2
• SU(2) groups have dimension groups have dimension dim=3,
• SO(3) groups have dimension dim=3;
• SU(3) groups have dimension dim=8

Εσωτερική Αρθρογραφία

• Ομάδα
• Ομαδοθεωρία
• Ορθογώνια Ομάδα
• Μοναδιακή Ομάδα
• Ετεροτική Ομάδα
• Αναπαράσταση
• Μήτρα
• Ομάδα E₈
• Adjoint representation
• Armand Borel
• Homogeneous space
• List of Lie group topics
• List of simple Lie groups
• Riemannian manifold
• Representations of Lie groups
• Table of Lie groups

Βιβλιογραφία

• Armand Borel, Essays in the history of Lie groups and algebraic groups, History of Mathematics 21, American Mathematical Society, 2001. ISBN 0-8218-0288-7

• Thomas Hawkins, Emergence of the theory of Lie groups, Springer, 2000. ISBN 0-387-98963-3

• Brian C. Hall Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, 2003. ISBN 0-387-40122-9

• N. Bourbaki, Elements of mathematics: Lie groups and Lie algebras Chapter 1-3 ISBN 3-540-64242-0, Chapters 4-6 ISBN 3-540-42650-7, Chapters 7-9 ISBN 3-540-43405-4

• C. Chevalley, Theory of Lie groups, ISBN 0-691-04990-4.

• J.-P. Serre. Lie Algebras and Lie Groups: 1964 Lectures given at Harvard University, LNM 1500, Springer. ISBN 3-540-55008-9

• Anthony W. Knapp, Lie Groups Beyond an Introduction, Second Edition. Birkhäuser, 2002.

• J.F. Adams, Lectures on Lie Groups (Chicago Lectures in Mathematics). ISBN 0-226-00527-5

• Representation Theory : A First Course (Graduate Texts in Mathematics / Readings in Mathematics) by William Fulton, Joe Harris Publisher: Springer; 1 edition (July 30, 1999) ISBN 0-387-97495-4

• Wulf Rossmann, Lie Groups: An Introduction Through Linear Groups (Oxford Graduate Texts in Mathematics), Oxford University Press ISBN 0-19-859683-9. The 2003 reprinting corrects some unfortunate typos.

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• scientificamerican
• edugate.gr
• An Exceptionally Simple Theory of Everything
• cmth.ph.ic.ac.uk
• Ανάλυση Ομάδας Lie
• Απλοϊκή Ανάλυση Ομάδας Lie
• Illustrating Geometry
• Lie groups, jakobsen

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---