Πρώτος Αριθμός
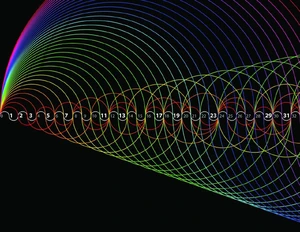
Prime number patterns.
A prime number is a natural number that
has no positive divisors other than 1 and itself.
There are twenty-five primes between one and a hundred;
168 between one and a thousand;
and 78.498 between one and a million.


Κυκλική Ομάδα
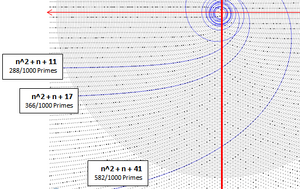
Πρώτος Αριθμός

Μαθηματική Πλάνη

Πρώτος Αριθμός
Actually, for all natural numbers n>1; (n-1)(n+1)=n^2-1. This is true for all pairs of natural numbers (n-1) & (n+1), whether they are twin primes or not.

Πρώτος Αριθμός
Πρώτος Αριθμός

Μοτίβο
Μαθηματική Πλάνη
- Ένα είδος Αριθμών
Ετυμολογία[]
Η ονομασία "πρώτος" σχετίζεται ετυμολογικά με την λέξη "πρωτείο".
Εισαγωγή[]
|
|
|---|
| Α. Αριθμοσύνολα |
---
|
| Β. Ειδικοί Αριθμοί |
|
| Γ. Άλλοι Αριθμοί |
|
| Δ. Ψηφία |
|
Οι πρώτοι αριθμοί είναι, για την Αριθμητική, ακριβώς ότι είναι για τη Φυσική τα θεμελιώδη σωματίδια της ύλης.
Είναι οι δομικοί λίθοι επί των οποίων κτίζονται όλοι οι υπόλοιποι αριθμοί.
Γενικά πρώτος αριθμός είναι εκείνος που δεν μπορεί να διαιρεθεί (ακριβώς) με κανέναν άλλο αριθμό εκτός από τη μονάδα και τον ίδιο του τον εαυτό.
Υπάρχουν πολλά ερωτήματα για αυτούς:
- Πώς μπορούμε να προβλέψουμε πότε θα προκύψει ο επόμενος πρώτος αριθμός;
- Υπάρχει κάποιος μαθηματικός τύπος που παράγει πρώτους αριθμούς;
- Ποιός είναι ο αλγόριθμος που γεννά αυτούς τους αριθμούς;
Από την εποχή των αρχαίων Ελλήνων μέχρι τις ημέρες μας, οι μαθηματικοί προσπαθούν να δώσουν απαντήσεις σε αυτά τα ερωτήματα, επιδιώκοντας να εξιχνιάσουν αυτό τον αρχετυπικό γρίφο.
Υπόθεση Riemann[]
Πριν από σχεδόν 150 έτη, το 1859, ο Γερμανός μαθηματικός Bernard Riemann, στην Ακαδημία του Βερολίνου, παρουσίασε ένα άρθρο σχετικά με τους πρώτους αριθμούς. Στον πυρήνα της παρουσίασής του βρισκόταν μια ιδέα -μια υπόθεση- που φαινόταν να αποκαλύπτει ότι υπήρχε μια κρυφή, μαγευτική αρμονία ανάμεσα στους πρώτους και στους υπόλοιπους αριθμούς.
Ο Riemann υποστήριζε ακράδαντα ότι η υπόθεσή του ήταν εντελώς αληθινή. Όμως, λίγο αργότερα, ο Ρίμαν απέθανε.
Αμέσως μετά το θάνατό του, η μισθώτριά του έκαψε όλες τις προσωπικές σημειώσεις του και μέχρι σήμερα, κανείς δεν έμαθε αν είχε όντως ανακαλύψει την απόδειξη.
Στην σύγχρονη εποχή η Υπόθεση Riemann έχει γίνει η υπ' αριθμόν ένα μονομανία για πολλούς κορυφαίους μαθηματικούς. Θεωρείται πολύ δυσκολότερη και αναμφίβολα σημαντικότερη από το Τελευταίο Θεώρημα Fermat και αν αποδεικνυόταν θα μπορούσε να αποτελέσει τον περιοδικό πίνακα για τη χαρτογράφηση ολόκληρου του Μαθηματικού Σύμπαντος.
Ωστόσο, οι συνέπειες της Υπόθεσης Riemann επεκτείνονται πέραν από τα Μαθηματικά. Έχουν σημαντικές επιπτώσεις στην οικονομική δραστηριότητα, αφού οι πρώτοι αριθμοί αποτελούν τη βάση για την ασφάλεια στις τραπεζικές συναλλαγές και το Ηλεκτρονικό Εμπόριο. Η Υπόθεση Riemann είναι ακόμα το σημείο συνάντησης πολλών επιστημονικών τομέων με διακλαδώσεις στην Κβαντική Φυσική, τη Θεωρία του Χάους και την Πληροφορική.
Σκαπανείς σε όλους αυτούς τους τομείς συναγωνίζονται για να απασφαλίσουν τον κώδικα, ενώ ένα βραβείο ενός εκατομμυρίου δολαρίων έχει αθλοθετηθεί για τον νικητή.
Μαθηματική Παρουσίαση[]
Στα μαθηματικά πρώτος αριθμός είναι ένας Φυσικός Αριθμός μεγαλύτερος της μονάδας με την ιδιότητα οι μόνοι φυσικοί διαιρέτες του να είναι η μονάδα και ο εαυτός του.
Το μηδέν και το ένα δεν είναι πρώτοι αριθμοί. Το μηδέν συχνά δεν θεωρείται ούτε φυσικός.
Η ακολουθία των πρώτων αρχίζει ως εξής: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113 ...
Ο αριθμός 2 είναι ο μόνος άρτιος πρώτος αριθμός. Όλοι οι άλλοι πρώτοι είναι περιττοί.
Αναπαράσταση φυσικών αριθμών[]
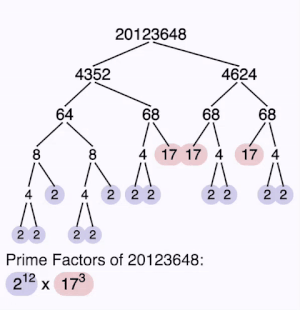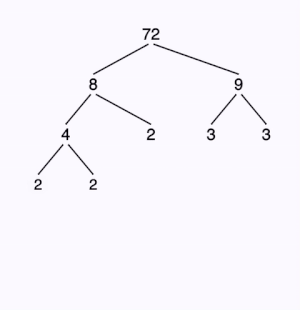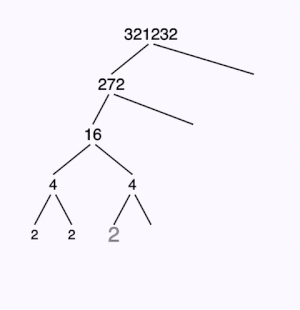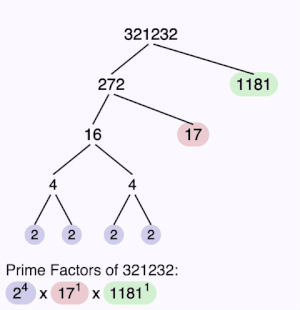
Το Θεμελιώδες Θεώρημα Αριθμητικής βεβαιώνει ότι κάθε θετικός ακέραιος γράφεται ως γινόμενο πρώτων παραγόντων με μοναδικό τρόπο.
Για παράδειγμα:
Πλήθος πρώτων[]
Οι πρώτοι αριθμοί έχουν άπειρο πλήθος. Η πρόταση αυτή έχει αποδειχθεί με διάφορους τρόπους. Η πρώτη γνωστή απόδειξη είναι του Ευκλείδη:
Έστω ότι οι πρώτοι έχουν πεπερασμένο πλήθος n και είναι οι . Ορίζουμε τον ακέραιο
αυτός ο αριθμός δεν διαιρείται με κανένα πρώτο και αυτό είναι άτοπο ΟΕΔ.
Εύρεση πρώτων[]
Η εύρεση των πρώτων αριθμών απασχόλησε από την αρχαιότητα τους μαθηματικούς. Ένας από τους πιο απλούς αλλά και αργούς τρόπους για (μαζική) εύρεση πολλών πρώτων είναι το λεγόμενο κόσκινο του Ερατοσθένη: Στο σύνολο των φυσικών αριθμών - πρακτικά έως κάποιο μεγάλο αριθμό Ν - αρχίζουμε και αποκλείουμε πρώτα τα πολλαπλάσια του 2 μετά τα πολλαπλάσια του επόμενου μη διαγραμμένου αριθμού κ.ο.κ. έως το Ν. Παρατηρούμε ότι όλο και λιγότερους αριθμούς θα βρίσκουμε προς διαγραφή.
Οι αριθμοί που θα απομείνουν είναι όλοι πρώτοι. Το κόσκινο του Ερατοσθένη είναι ένας αργός αλγόριθμος για το άν ένας συγκεκριμένος αριθμός Ν είναι πρώτος ή όχι, διότι μεταξύ άλλων απαιτεί ουσιαστικά και την εύρεση όλων των πρώτων μικρότερων ίσων του (αν ένας αριθμός Ν δεν έχει διαιρέτες μικρότερους ίσους του , τοτε έναι πρώτος).
Άλλοι Αλγόριθμοι[]
Παρατίθενται μερικοί αλγόριθμοι (κατά σειρά ταχύτητας ή και απλότητας) για την εύρεση άν ο Ν>=2 είναι πρώτος. Η σειρά επίσης αυτών των αλγορίθμων είναι παιδευτική για την εισαγωγή σε μια σειρά από προγράμματα για ηλεκτρονικούς υπολογιστές.
Απλός 1[]
- Εξετάζουμε διαδοχικά όλους τους ακέραιους Μ < Ν
- Μόλις βρεθεί διαιρέτης του Ν σταματάμε και ο Ν δεν είναι πρώτος
- Αν εξαντληθούν οι Μ χωρίς να βρεθεί διαιρέτης, τότε ο Ν είναι πρώτος
Απλός 2[]
Βασιζόμενοι στην παρατήρηση ότι κανένας αριθμός Ν δεν έχει διαιρέτη μεγαλύτερο του Ν/2, τροποποιούμε τον παραπάνω αλγόριθμο εξετάζοντας όλους τους αριθμούς Μ<Ν/2.
Απλός 3[]
Παρατηρούμε ότι αν ένας αριθμός Ν δεν είναι πρώτος τότε έχει (τουλάχιστον) δύο διαιρέτες μεγαλύτερους από 1. Παρατηρούμε ότι σε αυτή την περίπτωση τουλάχιστον ένας διαιρέτης είναι μικρότερος από την τετραγωνική ρίζα του αριθμού. Τροποποιούμε τον παραπάνω αλγόριθμο εξετάζοντας όλους τους αριθμούς Μ < αν το δεν είναι ακέραιος. Αλλιώς ο αριθμός δεν είναι πρώτος αφού τον διαιρεί και η τετραγωνική του ρίζα.
Ο μέγιστος γνωστός πρώτος αριθμός[]
Στις 4 Σεπτεμβρίου 2006 ανακαλύφθηκε ο μεγαλύτερος γνωστός πρώτος αριθμός.
Είναι ο και έχει 9.808.358 ψηφία.
Έχει 650.000 περισσότερα ψηφία από τον προηγούμενο μεγαλύτερο πρώτο αριθμό, που είχε βρεθεί τον Δεκέμβριο του 2005.
Τον ανακάλυψαν οι Κέρτις Κούπερ και Στίβεν Μπουν, καθηγητές του Κρατικού Πανεπιστημίου του Κεντρικού Μιζούρι, μέσω του προγράμματος GIMPS (Great Internet Mersenne Prime Search).
Ιδιότητες πρώτων[]
- Αν ο p είναι πρώτος και διαιρεί το γινόμενο ab γιά κάποιους ακέραιους a, b τότε ο p διαιρεί το a ή το b. (Ευκλείδης)
- Αν p πρώτος και a ακέραιος, τότε το ap − a διαιρείται από το p (Μικρό Θεώρημα του Φερμά).
- Ένας ακέραιος p > 1 είναι πρώτος αν και μόνο αν p - 1 παραγοντικό + 1 δηλ. το (p − 1)! + 1 διαιρείται από το p (Θεώρημα του Ουίλσον).
Ανοικτά ερωτήματα[]
Ένα από τα ανοικτά ερωτήματα της σύγχρονης θεωρίας αριθμών είναι το πρόβλημα της παραγοντοποίησης μεγάλων ακεραίων, δηλαδή της εύρεσης αλγορίθμου παραγοντοποίησης σε πολυωνυμικό χρόνο. Στην "σκιά" αυτού του προβλήματος αναπτύχθηκε η κρυπτογραφία δημόσιου κλειδιού και ειδικότερα του κρυπτοσυστήματος RSA.
Oι εικασίες του Γκόλντμπαχ[]
Είναι πολύ γνωστή η πρώτη εικασία που διατύπωσε ο Κρίστιαν Γκόλντμπαχ 1690 - 1764 , η οποία σχετίζεται με τους πρώτους αριθμούς. Ο Γκόλντμπαχ υποστήριξε οτι κάθε άρτιος αριθμός μεγαλύτερος του 2, μπορεί να γραφεί ως άθροισμα δύο πρώτων αριθμών. Η απόδειξη της παραπάνω εικασίας ταλανίζει ακόμα και σήμερα τους μαθηματικούς, καθώς παράλληλα οι υπολογιστές επιβεβαιώνουν την εικασία για όλο και μεγαλύτερους αριθμούς. Το 1998, η εικασία επιβεβαιώθηκε για αριθμούς μέχρις και της τάξης του
Η δεύτερη εικασία του Γκόλντμπαχ έγκειται στο ότι κάθε περιττός αριθμός μεγαλύτερος του 6 είναι άθροισμα τριών πρώτων αριθμών. Και αυτή η εικασία παραμένει αναπόδεικτη, αν και επιβεβαιώνεται από ηλεκτρονικούς υπολογιστές. Τυχόν απόδειξη της πρώτης εικασίας του Γκόλντμπαχ θα αποδείκνυε αμέσως και τη δεύτερη εικασία.
Υποσημειώσεις[]
Εσωτερική Αρθρογραφία[]
Βιβλιογραφία[]
Ιστογραφία[]
|
Αν και θα βρείτε εξακριβωμένες πληροφορίες "Οι πληροφορίες αυτές μπορεί πρόσφατα Πρέπει να λάβετε υπ' όψη ότι Επίσης, |
- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν
- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)






