Ρητός Αριθμός

Ρητός Αριθμός

Rational Number

Ρητός Αριθμός

Πραγματικός Αριθμός
Ρητός Αριθμός
Άρρητος Αριθμός

Διακριτά Μαθηματικά
Αριθμητική
Αριθμοθεωρία
Αριθμός
Μαθηματική Πράξη
Τελεστής

- Ένα είδος αριθμών.

Ετυμολογία

Αριθμοί
Α. Αριθμοσύνολα
Φυσικός Αριθμός Number Ακέραιος Αριθμός Number Ρητός Αριθμός Number Άρρητος Αριθμός Number Υπερβατικός Αριθμός Number Πραγματικός Αριθμός Number Φανταστικός Αριθμός Number Μιγαδικός Αριθμός Number Άρτιος Αριθμός Number Περιττός Αριθμός Number Θετικός Αριθμός Number Αρνητικός Αριθμός Number --- Αλγεβρικός Αριθμός Number Πρώτος Αριθμός Number
Β. Ειδικοί Αριθμοί
Μηδενικός Αριθμός Number Μοναδιαίος Αριθμός Number Αριθμός i Number Αριθμός π Number Αριθμός e Number
Γ. Άλλοι Αριθμοί
Αντίστροφος Αριθμός Number Αντίθετος Αριθμός Number Ασύμμετρος Αριθμός Number Περιοδικός Αριθμός Number Απεριοδικός Αριθμός Number Δεκαδικός Αριθμός Number Κλασματικός Αριθμός Number Σιμμιγής Αριθμός Number Κβαντικός Αριθμός Number Μαγικός Αριθμός Number Χρυσός Αριθμός Number Αποκαλυπτικός Αριθμός Number
Δ. Ψηφία
Ένα Number Δύο Number Τρία Number Τέσσερα Number Πέντε Number Έξι Number Επτά Number Οκτώ Number Εννέα Number Δέκα Number Εκατό Number Χίλια Number Εκατομμύριο Number

Η ονομασία "Ρητός" σχετίζεται ετυμολογικά με την λέξη "ρήση".

Εισαγωγή

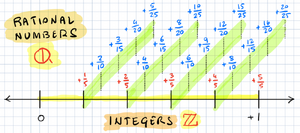
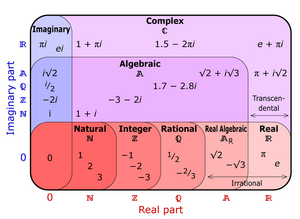
Το σύνολο των ρητών αριθμών είναι το σύνολο των αριθμών που μπορούν να γραφούν σε μορφή κλάσματος με ακέραιους όρους και παρονομαστή διάφορο του μηδενός.

Συμβολίζεται με $\mathbb{Q}$. Το σύνολο των ρητών περιγράφεται από το σύνολο:

$\left\{\frac{\mu}{\nu} : \mu \in \mathbb{Z}, \nu \in \mathbb{Z}, n \ne 0 \right\}$

και ισοδύναμα από το:

$\left\{\frac{\mu}{\nu} : \mu \in \mathbb{Z}, \nu \in \mathbb{N} \right\}$

Το σύνολο των ρητών αριθμών αποτελεί ένα διατεταγμένο σώμα. Είναι το μικρότερο σώμα με χαρακτηριστική 0 και για το λόγο αυτό είναι "πρώτο σώμα".

Όλοι οι ρητοί αριθμοί μπορούν να γραφούν με άπειρους διαφορετικούς τρόπους ως πηλίκα δύο ακεραίων μ/ν όπου το ν δεν είναι ίσο με μηδέν. Αποδεικνύεται ότι υπάρχει μοναδικός τρόπος γραφής κάθε ρητού στην μορφή μ/ν με ν φυσικό, όπου ο Μέγιστος Κοινός Διαιρέτης, μκδ(μ, ν) των μ και ν είναι η μονάδα η οποία είναι και η απλούστερη μορφή του.

Η δεκαδική αναπαράσταση κάθε ρητού αριθμού είναι πάντα περιοδική.

Το σύνολο των ρητών είναι γνήσιο υποσύνολο αυτού των πραγματικών αριθμών, υπάρχουν δηλαδή πραγματικοί αριθμοί που δεν είναι ρητοί. Οι αριθμοί αυτοί ονομάζονται άρρητοι.

Επιπλέον το σύνολο των ακεραίων και κατά συνέπεια και το σύνολο των φυσικών, είναι υποσύνολο αυτού των ρητών αφού κάθε ακέραιος α γράφεται στη μορφή α/1 που είναι ρητός.

Αριθμητική

Δύο ρητοί αριθμοί $\frac{\alpha}{\beta}$ και $\frac{\gamma}{\delta}$ καλούνται ίσοι δηλ. $\frac{\alpha}{\beta} = \frac{\gamma}{\delta}$ αν και μόνο αν $\alpha\delta= \beta\gamma$

Γενικά οι ρητοί αριθμοί όπως και οι ακεραίοι ικανοποιούν:

• την αντιμεταθετική ως προς την πρόσθεση και τον πολλαπλασιασμό
• την Προσεταιριστική Ιδιότητα ως προς την πρόσθεση και τον πολλαπλασιασμό και
• την Επιμεριστική Ιδιότητα του πολλαπλασιασμού ως προς την πρόσθεση.

Η πρόσθεση δύο ρητών ορίζεται ως ακολούθως:

$\frac{\alpha}{\beta} + \frac{\gamma}{\delta} = \frac{\alpha\delta + \beta\gamma}{\beta\delta}$

Ο πολλαπλασιασμός δύο ρητών ορίζεται ως ακολούθως:

$\frac{\alpha}{\beta} \cdot \frac{\gamma}{\delta} = \frac{\alpha\gamma}{\beta\delta}$

Ιδιότητες

• Το σύνολο των ρητών αριθμών είναι αριθμήσιμο.

• Το σύνολο των ρητών αριθμών είναι πυκνό στο σύνολο των πραγματικών. Με αυτό εννοούμε ότι μεταξύ δύο οποιονδήποτε πραγματικών μπορεί να ανευρεθεί πάντοτε ένας ρητός και κατά συνέπεια μεταξύ δύο πραγματικών αριθμών μπορούν να ανευρεθούν άπειροι σε πλήθος ρητοί αριθμοί.

Επίσης είναι εύκολο να αποδείξει κανείς ότι και μεταξύ δύο οποιονδήποτε ρητών αριθμός μπορεί να ανευρεθεί τουλάχιστον ένας άλλος ρητός αριθμός και κατά συνέπεια άπειροι σε πλήθος ρητοί.

Εσωτερική Αρθρογραφία

• Αριθμός
• Αριθμοσύνολο

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---