Τανυστής Einstein

Τανυστής Einstein

Einstein tensor

Σχετικιστική Φυσική

---

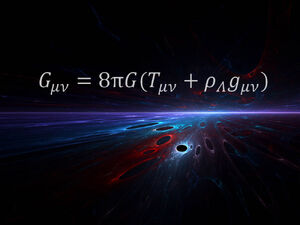
Πεδιακές Εξισώσεις Einstein Γενική Σχετικότητα Σχετικότητα

---

Βαρυτικό Πεδίο Τανυστής Einstein Τανυστής Ricci Κοσμολογική Σταθερά Κοσμολογία Θεωρία Διαστολής Σύμπαντος

Είναι ένα Φυσικό Μέγεθος.

Ετυμολογία

Η ονομασία "Τανυστής Einstein" σχετίζεται ετυμολογικά με την λέξη "ενέργεια".

Εισαγωγή

Ο τανυστής Einstein προσδιορίζει, µέσω των Εξισώσεων Πεδίου της Γενικής Θεωρίας της Σχετικότητας, την καμπυλότητα σε κάθε σηµείο του Χωροχρόνου, λόγω της παρουσίας ύλης (µε τη µορφή µάζας ή ενέργειας) στο σηµείο εκείνο.

To Βαρυτικό Πεδίο ϑεωρείται αποτέλεσµα της καµπύλωσης του χώρου λόγω της ύλης και η αλληλεπίδραση γεωµετρίας και ύλης περιγράφεται από τις εξισώσεις Einstein.

Ορισμός

Στην Διαφορική Γεωμετρία (differential geometry), ο τανυστής Einstein $\mathbf{G}$ είναι ένας τανυστής 2ης τάξης (rank) οριζόμενος σε Πολύπτυχα Riemann (manifolds).

Με "άδεικτη σημειογραφία" (index-free notation) ορίζεται ως ακολούθως:

$\mathbf{G}=\mathbf{R}-\frac{1}{2}\mathbf{g}R,$

Όπου:

• $\mathbf{R}$ είναι ο Τανυστής Ricci ,
• $\mathbf g$ είναι ο Μετρικός Τανυστής and
• $R$ είναι η Βαθμωτή Καμπυλότητα.

Με "ένδεικτη σημειογραφία" (component form), η προηγούμενη εξίσωση γράφεται:

$G_{\mu\nu} = R_{\mu\nu} - {1\over2} g_{\mu\nu}R.$

Αναλυτική Μορφή

Ο Τανυστής Ricci εξαρτάται από τον μετρικό τανυστή, έτσι ο τανυστής Einstein μπορεί να ορισθεί άμεσα εκφραζόμενος μόνον από αυτόν.

Όμως, αυτή η έκφραση είναι πολύπλοκη. The complexity of this expression can be shown using the formula for the Ricci tensor in terms of Christoffel symbols:

$G_{\alpha\beta} = R_{\alpha\beta} - \frac{1}{2} g_{\alpha\beta} R$

$= R_{\alpha\beta} - \frac{1}{2} g_{\alpha\beta} g^{\gamma\zeta} R_{\gamma\zeta}$

$= (\delta^\gamma_\alpha \delta^\zeta_\beta - \frac{1}{2} g_{\alpha\beta}g^{\gamma\zeta}) R_{\gamma\zeta}$

$= (\delta^\gamma_\alpha \delta^\zeta_\beta - \frac{1}{2} g_{\alpha\beta}g^{\gamma\zeta})(\Gamma^\epsilon_{\gamma\zeta,\epsilon} - \Gamma^\epsilon_{\gamma\epsilon,\zeta} + \Gamma^\epsilon_{\epsilon\sigma} \Gamma^\sigma_{\gamma\zeta} - \Gamma^\epsilon_{\zeta\sigma} \Gamma^\sigma_{\epsilon\gamma})$

όπου :

• $\delta^\alpha_\beta$ είναι ο Τανυστής Kronecker.

Το Σύμβολο Christoffel $\Gamma^\alpha_{\beta\gamma}$ ορίζεται ως κάτωθι:

$\Gamma^\alpha_{\beta\gamma} = \frac{1}{2} g^{\alpha\epsilon}(g_{\beta\epsilon,\gamma} + g_{\gamma\epsilon,\beta} - g_{\beta\gamma,\epsilon})$

Χρήση στην Γενική Σχετικότητα

The Einstein tensor allows a compact expression of the Πεδιακές Εξισώσεις Einstein :

$G_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}.$

Using geometrized units, this simplifies to

$G_{\mu\nu} = 8 \pi \, T_{\mu\nu}.$

Από τον ανωτέρω αναλυτικό τύπο μπορεί να θεωρηθεί ότι ο τανυστής Einstein αποτελεί μία μη-γραμμική ( nonlinear) συνάρτηση του μετρικού τανυστή (metric tensor), αλλά στην πραγματικότητα είναι γραμμική συνάρτηση των δεύτερων μερικών παραγώγων του.

Ως συμμετρικός τανυστής 2ης τάξης (symmetric 2nd rank tensor), ο τανυστής Einstein έχει 10 ανεξάρτητες συνιστώσες σε ένα τετραδιάστατο Χώρο. It follows that the Einstein field equations are a set of 10 quasilinear second-order partial differential equations for the metric tensor.

Οι Ταυτότητες Bianchi can also be easily expressed with the aid of the Einstein tensor:

$\nabla_{\mu} G^{\mu\nu} = 0.$

The Bianchi identities automatically ensure the conservation of the τανυστής ενέργειας-ορμής (stress-energy tensor]] in curved spacetimes:

$\nabla_{\mu} T^{\mu\nu} = 0.$

The geometric significance of the Einstein tensor is highlighted by this identity. In coordinate frames respecting the gauge condition

$\Gamma^{\rho}_{\mu\nu} G^{\mu\nu} = 0$

an exact conservation law for the stress tensor density can be stated:

$\partial_{\mu}(\sqrt{g} T^{\mu\nu}) = 0$.

The Einstein tensor plays the role of distinguishing these frames.

Εσωτερική Αρθρογραφία

• τανυστής
• ενέργεια
• ορμή

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• dspace.lib.ntua.gr
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---