Υδροδυναμική

Υδροδυναμική

Hydrodynamics

Φυσική

---

Φυσικοί Γης
Νόμοι Φυσικής
Νόμοι Φυσικής
Θεωρίες Φυσικής
Πειράματα Φυσικής
Παράδοξα Φυσικής

Σχετικιστική Υδροδυναμική

Υδροδυναμική
Εκροή

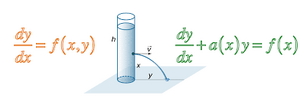
Ροή
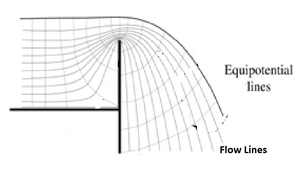
Ισοσταθμική Επιφάνεια

Μαγνητοϋδροδυναμική

Επιστήμη Επιστήμες

---

Φυσικές Επιστήμες Βιο-Επιστήμες Γεω-Επιστήμες Οικονομικές Επιστήμες Θεωρητικές Επιστήμες Κοινωνικές Επιστήμες Επιστήμες Υγείας

---

Τεχνολογία

---

Επιστημονικός Κλάδος Επιστημονικός Νόμος Επιστημονική Μέθοδος Επιστημονική Θεωρία Επιστημονικά Κέντρα Γης Επιστήμονες Γης

Εξισώσεις Navier-Stokes Υδροδυναμική

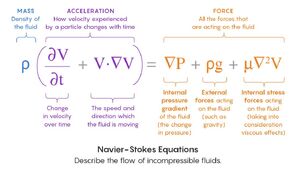
- Ένας Επιστημονικός Κλάδος της Κλασσικής Φυσικής

Ετυμολογία

Η ονομασία "Υδροδυναμική" σχετίζεται ετυμολογικά με την λέξη "Ύδωρ".

Εισαγωγή

Ο επιστημονικός κλάδος αυτός έχει ως αντικείμενο έρευνας και μελέτης τους νόμους που διέπουν την κίνηση των ασυμπίεστων υγρών όπως τη ροή των ρευστών, την ταχύτητα αυτών, την διεύθυνση των αγωγών ή φλεβών, την παροχή τους, τις διάφορες πιέσεις αυτών κ.λπ. καθώς επίσης και την συμπεριφορά των διαφόρων σωμάτων (αντιστάσεις) που εμφανίζουν κατά την κίνησή τους μέσα στα υγρά.

Βασικά θεωρήματα

Εξίσωση Συνέχειας

Ο Νόμος της συνέχειας της ροής είναι από τους σημαντικότερους νόμους της Υδροδυναμικής.

Η σχέση που περιγράφει αυτόν τον νόμο ονομάζεται εξίσωση της συνέχειας της ροής και αναφέρει ότι η παροχή παραμένει σταθερή κατά μήκος μίας φλέβας (ενός σωλήνα), που διαρρέεται από υγρό.

Η εξίσωση αυτή είναι άμεση συνέπεια της αρχής διατήρησης της ύλης.

Η μαθηματική της έκφραση είναι:

$\mathbf{A_1 u_1 = A_2 u_2}$

Όπου Α η διατομή του σωλήνα και u η ταχύτητα του υγρού

Παράδειγμα: Έστω ότι παρατηρείται ένας υδραγωγός που σε κάποιο σημείο του (1) παρουσιάζει μια ιδιαίτερη στένωση, είτε από εξωτερική παραμόρφωση, είτε εσωτερικά από εναπόθεση αλάτων, και τα σημεία 2 και 3 κοντά και εκατέρωθεν του 1, καθώς επίσης τα σημεία 4 και 5 εκατέρωθεν και μακρύτερα των προηγουμένων 2 και 3 αντίστοιχα. Θα διαπιστωθεί αμέσως ότι ο υδραγωγός αυτός είναι "μεταβλητής διατομής" αφού οι διατομές του στα σημεία 1, 2, 3, 4 και 5 είναι διάφορες. Λαμβάνοντας λοιπόν υπόψη ότι το το μεν υγρό είναι ασυμπίεστο και η ροή μόνιμη θα πρέπει σε ορισμένο χρόνο, σύμφωνα με την "Αρχή της συνεχείας της ροής", να διέρχεται από κάθε διατομή ίσος όγκος ρευστού.

Επειδή η παροχή Q = F υ θα έχουμε F₁ υ₁ = F₂ υ₂ = F₃ υ₃ = F₄ υ₄ = F₅ υ₅ = ............C σταθερό, ή γενικά, F υ = σταθερό.

Εξίσωση Bernoulli

Η εξίσωση αυτή διατυπώθηκε από τον Ελβετό φυσικό Daniel Bernoulli και είναι αποτέλεσμα της αρχής διατήρησης της ενέργειας σε κινούμενο υγρό.

Σύμφωνα με αυτή σε μία ρευματική γραμμή το άθροισμα της δυναμικής ενέργειας ανα μονάδα όγκου, της κινητικής ενέργειας ανά μονάδα όγκου και της πίεσης παραμένουν σταθερά, σε οποιοδήποτε σημείο μίας ρευματικής γραμμής.

δηλαδή ισχύει:

$P + \frac{1}{2}\rho u^2 +\rho g h$ = σταθ

Θέματα - Τομείς

• Νόμος διατηρήσεως μάζας,
• εξίσωση συνεχείας,
• Εξισώσεις κινήσεως.
• Νόμος διατηρήσεως της ορμής.
• Κλειστοί αγωγοί.
• Σταθερή τυρβώδης ροή σε σωλήνες,
• Συντελεστής τριβών f των Darcy – Weishbach.
• Ροή ιδεατού ρευστού,
• εξισώσεις Euler
• Εξισώσεις Bernoulli.
• Στροβιλότητα και δυναμικό ταχύτητας,
• ροϊκή συνάρτηση,
• εξίσωση Laplace.
• Ροή πραγματικών ρευστών,
• στρωτή-τυρβώδης ροή.
• Ροή υπεράνου στερεού ορίου, οριακό στρώμα.
• Ρευστομηχανικές δυνάμεις.
• Διαστατική ανάλυση, Θεώρημα Buckingham.
• Υδραυλική ομοιότητα.

Εσωτερική Αρθρογραφία

• Κλασσική Φυσική
• Κλασσική Μηχανική
• Κινηματική
• Στατική

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---