Χώρος Lebesgue

Χώρος Lebesgue

Lebesgue Space

Εσωτερικός Πολλαπλασιασμός
Χώρος Hilbert
Χώρος Lebesgue

Χώρος Hilbert
Χώρος Lebesgue

Μαθηματικά Γεωμετρία Γραμμική Άλγεβρα

---

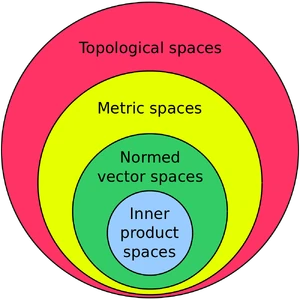
Γεωμετρικός Χώρος Ευκλείδειος Χώρος Χώρος Minkowski Χώρος Riemann Χώρος Lobachevsky

---

Μαθηματικός Χώρος Τοπολογικός Χώρος Διανυσματικός Χώρος Μετρικός Χώρος Χώρος Hilbert

Ελλειπτικός Χώρος Ευκλείδειος Χώρος Υπερβολικός Χώρος

Ελλειπτικός Χώρος Ευκλείδειος Χώρος Υπερβολικός Χώρος

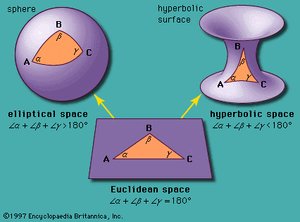
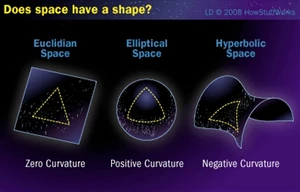
- Ένας Μαθηματικός Χώρος.

Ετυμολογία

Η ονομασία "Χώρος Lebesgue" σχετίζεται ετυμολογικά με το όνομα του μαθηματικού "Lebesgue".

Εισαγωγή

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces.

They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).

Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.

Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.

---

An Lp space may be defined as a space of functions for which the p-th power of the absolute value is Lebesgue integrable

L² is the only Hilbert space among L^p spaces.

In the complex case, the inner product on L² is defined by

$\langle f,g\rangle =\int _{S}f(x){\overline {g(x)}}\,\mathrm {d} \mu (x)$

The additional inner product structure allows for a richer theory, with applications to, for instance, Fourier series and quantum mechanics.

Functions in L² are sometimes called quadratically integrable functions, square-integrable functions or square-summable functions, but sometimes these terms are reserved for functions that are square-integrable in some other sense, such as in the sense of a Riemann integral.

If we use complex-valued functions, the space L^∞ is a commutative C*-algebra with pointwise multiplication and conjugation.

For many measure spaces, including all sigma-finite ones, it is in fact a commutative von Neumann algebra.

An element of L^∞ defines a bounded operator on any L^p space by multiplication.

Πίνακας Αντιστοιχίας

Σύγκριση Κλασσικού Κόσμου & Κβαντικού Κόσμου
1.	Φύση	Κλασσικό Σωματίδιο ---- Τροχιά	Κβαντικό Σωματίδιο ---- Κβαντική Κατάσταση
2.	Φυσική	Θέση (x)	Κυματοσυνάρτηση (ψ(x))
3.	Γεωμετρία	Σημείο του τρισ-διάστατου Γεωμετρικού Ευκλείδειου Χώρου	Σημείο του ν-διάστατου (Γεωμετρικού) Χώρου Hilbert (ℋ)
4.	Άλγεβρα	Στοιχείο (δηλ. τριάδα συναρτήσεων) του τρισ-διάστατου Αλγεβρικού Ευκλείδειου Χώρου	Στοιχείο (δηλ. νιάδα συναρτήσεων) του ν-διάστατου (Αλγεβρικού) Χώρου Lebesgue (ℒ²)

Εσωτερική Αρθρογραφία

• Μαθηματικός Χώρος
• Συναρτησιακή Ανάλυση

Ιστογραφία

• Ομώνυμο άρθρο στην Βικιπαίδεια
• Ομώνυμο άρθρο στην Livepedia
• [ ]
• [ ]

Κίνδυνοι Χρήσης

Αν και θα βρείτε εξακριβωμένες πληροφορίες σε αυτήν την εγκυκλοπαίδεια ωστόσο, παρακαλούμε να λάβετε σοβαρά υπ' όψη ότι η "Sciencepedia" δεν μπορεί να εγγυηθεί, από καμιά άποψη, την εγκυρότητα των πληροφοριών που περιλαμβάνει. "Οι πληροφορίες αυτές μπορεί πρόσφατα να έχουν αλλοιωθεί, βανδαλισθεί ή μεταβληθεί από κάποιο άτομο, η άποψη του οποίου δεν συνάδει με το "επίπεδο γνώσης" του ιδιαίτερου γνωστικού τομέα που σας ενδιαφέρει." Πρέπει να λάβετε υπ' όψη ότι όλα τα άρθρα μπορεί να είναι ακριβή, γενικώς, και για μακρά χρονική περίοδο, αλλά να υποστούν κάποιο βανδαλισμό ή ακατάλληλη επεξεργασία, ελάχιστο χρονικό διάστημα, πριν τα δείτε. Επίσης, Οι διάφοροι "Εξωτερικοί Σύνδεσμοι (Links)" (όχι μόνον, της Sciencepedia αλλά και κάθε διαδικτυακού ιστότοπου (ή αλλιώς site)), αν και άκρως απαραίτητοι, είναι αδύνατον να ελεγχθούν (λόγω της ρευστής φύσης του Web), και επομένως είναι ενδεχόμενο να οδηγήσουν σε παραπλανητικό, κακόβουλο ή άσεμνο περιεχόμενο. Ο αναγνώστης πρέπει να είναι εξαιρετικά προσεκτικός όταν τους χρησιμοποιεί.

- Μην κάνετε χρήση του περιεχομένου της παρούσας εγκυκλοπαίδειας
αν διαφωνείτε με όσα αναγράφονται σε αυτήν

---

>>Διαμαρτυρία προς την wikia<<

- Όχι, στις διαφημίσεις που περιέχουν απαράδεκτο περιεχόμενο (άσεμνες εικόνες, ροζ αγγελίες κλπ.)

---