https://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD,_%D0%98%D1%81%D0%B0%D0%B0%D0%BA

| Исаак Ньютон | |
| Isaac Newton | |
| GodfreyKneller-IsaacNewton-1689.jpg Портрет кисти Кнеллера (1689) | |
| Дата рождения: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
|---|---|
| Место рождения: |
Вулсторп, Линкольншир, Королевство Англия |
| Дата смерти: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
| Место смерти: |
Кенсингтон, Мидлсекс, Англия, Королевство Великобритания |
| Страна: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
| Научная сфера: | |
| Место работы: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
| Учёная степень: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
| Альма-матер: | |
| Научный руководитель: |
И. Барроу |
| Известные ученики: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
| Сайт: |
Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). |
| Подпись: |
Isaac Newton signature.svg |
| Ошибка Lua в Модуль:Wikidata на строке 124: attempt to index field 'wikibase' (a nil value). | |
Ошибка Lua в Модуль:CategoryForProfession на строке 52: attempt to index field 'wikibase' (a nil value).
Сэр Исаа́к Нью́тон (или Ньюто́н[K 1]) (англ. Sir Isaac Newton, 25 декабря 1642 года — 20 марта 1727 года по юлианскому календарю, действовавшему в Англии до 1752 года; или 4 января 1643 года — 31 марта 1727 года по григорианскому календарю) — английский физик[[Категория:Физики Великобритании]][[Категория:Физики XVII века]][[Категория:Физики XVIII века]], математик[[Категория:Математики Великобритании]][[Категория:Математики XVII века]][[Категория:Математики XVIII века]], механик [[Категория:Механики Великобритании]] [[Категория:Механики XVII века]] [[Категория:Механики XVIII века]] и астроном[[Категория:Астрономы Великобритании]][[Категория:Астрономы XVII века]][[Категория:Астрономы XVIII века]], один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.
Биография[]
Ранние годы[]

Исаак Ньютон родился в деревне Вулсторп (англ. Woolsthorpe, графство Линкольншир) в канун гражданской войны. Отец Ньютона, мелкий, но преуспевающий фермер Исаак Ньютон (1606—1642), не дожил до рождения сына. Мальчик родился преждевременно, был болезненным, поэтому его долго не решались крестить[1]. И всё же он выжил, был крещён (1 января[K 2]), и назван Исааком в память об отце. Факт рождения под Рождество Ньютон считал особым знаком судьбы[2]. Несмотря на слабое здоровье в младенчестве, он прожил 84 года.
Ньютон искренне считал, что его род восходит к шотландским дворянам XV века, однако историки обнаружили, что в 1524 году его предки были бедными крестьянами[3]. К концу XVI века семья разбогатела и перешла в разряд йоменов (землевладельцев). Отец Ньютона оставил в наследство крупную по тем временам сумму в 500 фунтов стерлингов и несколько сот акров плодородной земли, занятой полями и лесами[2].
В январе 1646 года мать Ньютона, Анна Эйскоу (англ. Hannah Ayscough)[K 3] (1623—1679) вновь вышла замуж. От нового мужа, 63-летнего вдовца, у неё было трое детей, и она стала уделять мало внимания Исааку. Покровителем мальчика стал его дядя по матери, Уильям Эйскоу. В детстве Ньютон, по отзывам современников, был молчалив, замкнут и обособлен, любил читать и мастерить технические игрушки: солнечные и водяные часы, мельницу и т. п. Всю жизнь он чувствовал себя одиноким[4].
Отчим умер в 1653 году, часть его наследства перешла к матери Ньютона и была сразу же оформлена ею на Исаака. Мать вернулась домой, однако основное внимание уделяла троим младшим детям и обширному хозяйству; Исаак по-прежнему был предоставлен сам себе.
В 1655 году 12-летнего Ньютона отдали учиться в расположенную неподалёку школу в Грэнтеме, где он жил в доме аптекаря Кларка. Вскоре мальчик показал незаурядные способности, однако в 1659 году мать Анна вернула его в поместье и попыталась возложить на 16-летнего сына часть дел по управлению хозяйством. Попытка не имела успеха — Исаак предпочитал всем другим занятиям чтение книг, стихосложение и особенно конструирование различных механизмов. В это время к Анне обратился Стокс, школьный учитель Ньютона, и начал уговаривать её продолжить обучение необычайно одарённого сына; к этой просьбе присоединились дядя Уильям и грэнтемский знакомый Исаака (родственник аптекаря Кларка) Хэмфри Бабингтон, член Кембриджского Тринити-колледжа. Объединёнными усилиями они, в конце концов, добились своего. В 1661 году Ньютон успешно окончил школу и отправился продолжать образование в Кембриджский университет.
Тринити-колледж (1661—1664)[]

Тринити-колледж, часовая башня
В июне 1661 года 18-летний Ньютон приехал в Кембридж. Согласно уставу, ему устроили экзамен на знание латинского языка, после чего сообщили, что он принят в Тринити-колледж (Колледж святой Троицы) Кембриджского университета. С этим учебным заведением связаны более 30 лет жизни Ньютона.
Колледж, как и весь университет, переживал трудное время. Только что (1660) в Англии была восстановлена монархия, король Карл II часто задерживал положенные университету выплаты, уволил значительную часть преподавательского состава, назначенную в годы революции[5]. Всего в Тринити-колледже проживало 400 человек, включая студентов, слуг и 20 нищих, которым по уставу колледж обязан был выдавать подаяние. Учебный процесс находился в плачевном состоянии[5].
Ньютона зачислили в разряд студентов-«сайзеров» (англ. sizar), с которых не брали платы за обучение (вероятно, по рекомендации Бабингтона). По нормам того времени, сайзер был обязан оплачивать своё обучение путём различных работ в Университете, либо путём оказания услуг более богатым студентам. Документальных свидетельств и воспоминаний об этом периоде его жизни сохранилось очень мало. В эти годы окончательно сложился характер Ньютона — стремление дойти до сути, нетерпимость к обману, клевете и угнетению, равнодушие к публичной славе. У него по-прежнему не было друзей[6].
В апреле 1664 года Ньютон, сдав экзамены, перешёл в более высокую студенческую категорию «школяров» (scholars), что дало ему право на стипендию и продолжение обучения в колледже.
Несмотря на открытия Галилея, естествознание и философию в Кембридже по-прежнему преподавали по Аристотелю. Однако в сохранившихся тетрадях Ньютона уже упоминаются Галилей, Коперник, картезианство, Кеплер и атомистическая теория Гассенди. Судя по этим тетрадям, он продолжал мастерить (в основном, научные инструменты), увлечённо занимался оптикой, астрономией, математикой, фонетикой, теорией музыки. Согласно воспоминаниям соседа по комнате, Ньютон беззаветно предавался учению, забывая про еду и сон; вероятно, несмотря на все трудности, это был именно тот образ жизни, которого он сам желал[7].

1664 год в жизни Ньютона был богат и другими событиями. Ньютон пережил творческий подъём, начал самостоятельную научную деятельность и составил масштабный список (из 45 пунктов) нерешённых проблем в природе и человеческой жизни (Вопросник, лат. Questiones quaedam philosophicae). В дальнейшем подобные списки не раз появляются в его рабочих тетрадях. В марте этого же года на недавно основанной (1663) кафедре математики колледжа начались лекции нового преподавателя, 34-летнего Исаака Барроу, крупного математика, будущего друга и учителя Ньютона. Интерес Ньютона к математике резко возрос. Он сделал первое значительное математическое открытие: биномиальное разложение для произвольного рационального показателя (включая отрицательные), а через него пришёл к своему главному математическому методу — разложению функции в бесконечный ряд[8]. В самом конце года Ньютон стал бакалавром.
Научной опорой и вдохновителями творчества Ньютона в наибольшей степени были физики: Галилей, Декарт и Кеплер. Ньютон завершил их труды, объединив в универсальную систему мира. Меньшее, но существенное влияние оказали другие математики и физики: Евклид, Ферма, Гюйгенс, Валлис и его непосредственный учитель Барроу. В студенческой записной книжке Ньютона есть программная фраза[9]:
В философии не может быть государя, кроме истины… Мы должны поставить памятники из золота Кеплеру, Галилею, Декарту и на каждом написать: «Платон — друг, Аристотель — друг, но главный друг — истина».
«Чумные годы» (1665—1667)[]
В канун Рождества 1664 года на лондонских домах стали появляться красные кресты — первые метки Великой эпидемии чумы. К лету смертоносная эпидемия значительно расширилась. 8 августа 1665 года занятия в Тринити-колледже были прекращены и персонал распущен до окончания эпидемии. Ньютон уехал домой в Вулсторп, захватив с собой основные книги, тетради и инструменты[10].
Это были бедственные годы для Англии — опустошительная чума (только в Лондоне погибла пятая часть населения), разорительная война с Голландией, Великий лондонский пожар. Но существенную часть своих научных открытий Ньютон сделал в уединении «чумных лет». Из сохранившихся заметок видно, что 23-летний Ньютон уже свободно владел базовыми методами дифференциального и интегрального исчислений, включая разложение функций в ряды и то, что впоследствии было названо формулой Ньютона-Лейбница. Проведя ряд остроумных оптических экспериментов, он доказал, что белый цвет есть смесь цветов спектра. Позже Ньютон вспоминал об этих годах[11]:
В начале 1665 года я нашёл метод приближённых рядов и правило превращения любой степени двучлена в такой ряд… в ноябре получил прямой метод флюксий[12] [дифференциальное исчисление]; в январе следующего года я получил теорию цветов, а в мае приступил к обратному методу флюксий [интегральное исчисление]… В это время я переживал лучшую пору своей юности и больше интересовался математикой и [натуральной] философией, чем когда бы то ни было впоследствии.
Но самым значительным его открытием в эти годы стал закон всемирного тяготения. Позднее, в 1686 году, Ньютон писал Галлею[13]:
В бумагах, написанных более 15 лет тому назад (точно привести дату я не могу, но, во всяком случае, это было перед началом моей переписки с Ольденбургом), я выразил обратную квадратичную пропорциональность тяготения планет к Солнцу в зависимости от расстояния и вычислил правильное отношение земной тяжести и conatus recedendi [стремление] Луны к центру Земли, хотя и не совсем точно.

Неточность, упомянутая Ньютоном, была вызвана тем, что размеры Земли и величину ускорения свободного падения Ньютон взял из «Механики» Галилея, где они приводились со значительной погрешностью[14]. Позднее Ньютон получил более точные данные Пикара и окончательно убедился в истинности своей теории[15].
Общеизвестна легенда о том, что закон тяготения Ньютон открыл, наблюдая падение яблока с ветки дерева. Впервые «яблоко Ньютона» мельком упомянул биограф Ньютона Уильям Стьюкли (книга «Воспоминания о жизни Ньютона», 1752 год)[16]:
После обеда установилась тёплая погода, мы вышли в сад и пили чай в тени яблонь. Он [Ньютон] сказал мне, что мысль о гравитации пришла ему в голову, когда он точно так же сидел под деревом. Он находился в созерцательном настроении, когда неожиданно с ветки упало яблоко. «Почему яблоки всегда падают перпендикулярно земле?» — подумал он.
Популярной легенда стала благодаря Вольтеру[17]. В действительности, как видно по рабочим тетрадям Ньютона, его теория всеобщего тяготения развивалась постепенно[10]. Другой биограф, Генри Пембертон, приводит рассуждения Ньютона (без упоминания яблока) более подробно: «сравнивая периоды нескольких планет и их расстояния до Солнца, он обнаружил, что… эта сила должна снижаться в квадратичной пропорциональности с увеличением расстояния»[17]. Другими словами, Ньютон обнаружил, что из третьего закона Кеплера, связывающего периоды обращения планет с расстоянием до Солнца, следует именно «формула обратных квадратов» для закона тяготения (в приближении круговых орбит). Окончательную формулировку закона тяготения, вошедшую в учебники, Ньютон выписал позднее, после того, как ему стали ясны законы механики.
Эти открытия, а также многие из позднейших, были опубликованы на 20-40 лет позже, чем были сделаны. Ньютон не гнался за славой. В 1670 году он писал Джону Коллинзу: «Я не вижу ничего желательного в славе, даже если бы я был способен заслужить её. Это, возможно, увеличило бы число моих знакомых, но это как раз то, чего я больше всего стараюсь избегать». Свой первый научный труд (октябрь 1666), излагавший основы анализа, он не стал публиковать; его нашли лишь спустя 300 лет[18].
Начало научной известности (1667—1684)[]

В марте-июне 1666 года Ньютон посетил Кембридж. Однако летом новая волна чумы вынудила его вновь уехать домой. Наконец, в начале 1667 года эпидемия утихла, и в апреле Ньютон возвратился в Кембридж. 1 октября он был избран членом Тринити-колледжа, а в 1668 году стал магистром. Ему выделили просторную отдельную комнату для жилья, назначили оклад (2 фунта в год) и передали группу студентов, с которыми он несколько часов в неделю добросовестно занимался стандартными учебными предметами. Впрочем, ни тогда, ни позже Ньютон не прославился как преподаватель, его лекции посещались плохо[19].
Упрочив своё положение, Ньютон совершил путешествие в Лондон, где незадолго до того, в 1660 году, было создано Лондонское королевское общество — авторитетная организация видных научных деятелей, одна из первых Академий наук. Печатным органом Королевского общества был журнал «Философские труды» (англ. Philosophical Transactions).
В 1669 году в Европе стали появляться математические работы, использующие разложения в бесконечные ряды. Хотя по глубине эти открытия не шли ни в какое сравнение с ньютоновскими, Барроу настоял на том, чтобы его ученик зафиксировал свой приоритет в этом вопросе. Ньютон написал краткий, но достаточно полный конспект этой части своих открытий, который назвал «Анализ с помощью уравнений с бесконечным числом членов». Барроу переслал этот трактат в Лондон. Ньютон просил Барроу не раскрывать имя автора работы[20] (но тот всё же проговорился). «Анализ» распространился среди специалистов и получил некоторую известность в Англии и за её пределами[21].
В этом же году Барроу принял приглашение короля стать придворным капелланом и оставил преподавание. 29 октября 1669 года 26-летний Ньютон был избран его преемником, профессором математики и оптики Тринити-колледжа, с высоким окладом 100 фунтов в год. Барроу оставил Ньютону обширную алхимическую лабораторию; в этот период Ньютон всерьёз увлёкся алхимией, провёл массу химических опытов[22].

Одновременно Ньютон продолжил эксперименты по оптике и теории цвета. Ньютон исследовал сферическую и хроматическую аберрации. Чтобы свести их к минимуму, он построил смешанный телескоп-рефлектор: линза и вогнутое сферическое зеркало, которое сделал и отполировал сам. Проект такого телескопа впервые предложил Джеймс Грегори (1663), однако этот замысел так и не был реализован. Первая конструкция Ньютона (1668) оказалась неудачной, но уже следующая, с более тщательно отполированным зеркалом, несмотря на небольшие размеры, давала 40-кратное увеличение превосходного качества[10].
Слухи о новом инструменте быстро дошли до Лондона, и Ньютона пригласили показать своё изобретение научной общественности. В конце 1671 — начале 1672 года прошла демонстрация рефлектора перед королём, а затем — в Королевском обществе. Аппарат вызвал всеобщие восторженные отзывы. Вероятно, сыграла свою роль и практическая важность изобретения: астрономические наблюдения служили для точного определения времени, что в свою очередь было необходимо для навигации на море. Ньютон стал знаменит и в январе 1672 года был избран членом Королевского общества. Позднее усовершенствованные рефлекторы стали основными инструментами астрономов, с их помощью были открыты планета Уран, иные галактики, красное смещение.
Первое время Ньютон дорожил общением с коллегами из Королевского общества, где состояли, кроме Барроу, Джеймс Грегори, Джон Валлис, Роберт Гук, Роберт Бойль, Кристофер Рен и другие известные деятели английской науки. Однако вскоре начались утомительные конфликты, которых Ньютон очень не любил. В частности, разгорелась шумная полемика по поводу природы света. Началась она с того, что в феврале 1672 года Ньютон опубликовал в «Philosophical Transactions» подробное описание своих классических опытов с призмами и свою теорию цвета. Гук, который ранее опубликовал собственную теорию, заявил, что результаты Ньютона его не убедили; его поддержал Гюйгенс на том основании, что теория Ньютона «противоречит общепринятым воззрениям». Ньютон ответил на их критику только через полгода, но к этому времени число критиков значительно увеличилось.
Лавина некомпетентных нападок вызвала у Ньютона раздражение и депрессию. Ньютон попросил секретаря Общества Ольденбурга больше не пересылать ему критических писем и дал зарок на будущее: не ввязываться в научные споры. В письмах он жалуется, что поставлен перед выбором: либо не публиковать свои открытия, либо тратить всё время и все силы на отражение недружелюбной дилетантской критики. В конце концов он выбрал первый вариант и сделал заявление о выходе из Королевского общества (8 марта 1673 года). Ольденбург не без труда уговорил его остаться[23], однако научные контакты с Обществом были надолго сведены к минимуму.
В 1673 году произошли два важных события. Первое: королевским указом в Тринити вернулся старый друг и покровитель Ньютона, Исаак Барроу, теперь в качестве руководителя («мастера») колледжа. Второе: математическими открытиями Ньютона заинтересовался Лейбниц, известный на тот момент как философ и изобретатель. Получив труд Ньютона 1669 года по бесконечным рядам и глубоко его изучив, он далее самостоятельно начал развивать свою версию анализа. В 1676 году Ньютон и Лейбниц обменялись письмами, в которых Ньютон разъяснил ряд своих методов, ответил на вопросы Лейбница и намекнул на существование ещё более общих методов, пока не опубликованных (имелось в виду общее дифференциальное и интегральное исчисления). Секретарь Королевского общества Генри Ольденбург настойчиво просил Ньютона во славу Англии опубликовать свои математические открытия по анализу, но Ньютон ответил, что уже пять лет как занимается другой темой и не хочет отвлекаться[24]. На очередное письмо Лейбница Ньютон не ответил. Первая краткая публикация по ньютоновскому варианту анализа появилась только в 1693 году, когда вариант Лейбница уже широко распространился по Европе.
Конец 1670-х годов был печален для Ньютона. В мае 1677 года неожиданно умер 47-летний Барроу. Зимой этого же года в доме Ньютона возник сильный пожар, и часть рукописного архива Ньютона сгорела. В сентябре 1677 года умер благоволивший Ньютону секретарь Королевского Общества Ольденбург, и новым секретарём стал Гук, относившийся к Ньютону неприязненно. В 1679 году тяжело заболела мать Анна; Ньютон, оставив все дела, приехал к ней, принимал активное участие в уходе за больной, но состояние матери быстро ухудшалось, и она умерла. Мать и Барроу были в числе немногих людей, скрашивавших одиночество Ньютона[25].
«Математические начала натуральной философии» (1684—1686)[]

История создания этого труда, одного из самых знаменитых в истории науки, началась в 1682 году, когда прохождение кометы Галлея вызвало подъём интереса к небесной механике. Эдмонд Галлей пытался уговорить Ньютона опубликовать его «общую теорию движения», о которой уже давно ходили слухи в учёном сообществе. Ньютон, не желая втягиваться в новые научные споры и пререкания, отказался.
В августе 1684 года Галлей приехал в Кембридж и рассказал Ньютону, что они с Реном и Гуком обсуждали, как из формулы закона тяготения вывести эллиптичность орбит планет, но не знали, как подступиться к решению. Ньютон сообщил, что у него уже есть такое доказательство, и в ноябре прислал Галлею готовую рукопись. Тот сразу оценил значение результата и метода, немедленно снова навестил Ньютона и на этот раз сумел уговорить его опубликовать свои открытия[13]. 10 декабря 1684 года в протоколах Королевского общества появилась историческая запись[26]:
Господин Галлей… недавно видел в Кембридже м-ра Ньютона, и тот показал ему интересный трактат «De motu» [О движении]. Согласно желанию г-на Галлея, Ньютон обещал послать упомянутый трактат в Общество.
Работа над книгой шла в 1684—1686 годах. По воспоминаниям Хэмфри Ньютона, родственника учёного и его помощника в эти годы, сначала Ньютон писал «Начала» в перерывах между алхимическими опытами, которым уделял основное внимание, затем постепенно увлёкся и с воодушевлением посвятил себя работе над главной книгой своей жизни[27].
Публикацию предполагалось осуществить на средства Королевского общества, но в начале 1686 года Общество издало не нашедший спроса трактат по истории рыб, и тем самым истощило свой бюджет. Тогда Галлей объявил, что он берёт расходы по изданию на себя. Общество с признательностью приняло это великодушное предложение и в качестве частичной компенсации бесплатно предоставило Галлею 50 экземпляров трактата по истории рыб[27].
Труд Ньютона — возможно, по аналогии с «Началами философии» Декарта (1644) или, по мнению некоторых историков науки, с вызовом картезианцам[28] — получил название «Математические начала натуральной философии» (лат. Philosophiae Naturalis Principia Mathematica), то есть, на современном языке, «Математические основы физики»[K 4].
28 апреля 1686 года первый том «Математических начал» был представлен Королевскому обществу. Все три тома, после некоторой авторской правки, вышли в 1687 году. Тираж (около 300 экземпляров) был распродан за 4 года — для того времени очень быстро.

Как физический, так и математический уровень труда Ньютона совершенно несопоставимы с работами его предшественников[29]. В нём отсутствует аристотелева или декартова метафизика, с её туманными рассуждениями и неясно сформулированными, часто надуманными «первопричинами» природных явлений. Ньютон, например, не провозглашает, что в природе действует закон тяготения, он строго доказывает этот факт, исходя из наблюдаемой картины движения планет и их спутников. Метод Ньютона — создание модели явления, «не измышляя гипотез», а потом уже, если данных достаточно, поиск его причин. Такой подход, начало которому было положено Галилеем, означал конец старой физики. Качественное описание природы уступило место количественному — значительную часть книги занимают расчёты, чертежи и таблицы.
В своей книге Ньютон ясно определил базовые понятия механики, причём ввёл несколько новых, включая такие важнейшие физические величины, как масса, внешняя сила и количество движения. Сформулированы три закона механики. Приведён строгий вывод из закона тяготения всех трёх законов Кеплера. Отметим, что были описаны и неизвестные Кеплеру гиперболические и параболические орбиты небесных тел. Истинность гелиоцентрической системы Коперника Ньютон прямо не обсуждает, но подразумевает; он даже оценивает отклонение Солнца от центра масс Солнечной системы[30]. Другими словами, Солнце в системе Ньютона, в отличие от кеплеровской, не покоится, а подчиняется общим законам движения. В общую систему включены и кометы, вид орбит которых вызывал тогда большие разногласия.
Слабым местом теории тяготения Ньютона, по мнению многих учёных того времени, было отсутствие объяснения природы этой силы. Ньютон изложил только математический аппарат, оставив открытыми вопросы о причине тяготения и его материальном носителе. Для научной общественности, воспитанной на философии Декарта, это был непривычный и вызывающий подход[29], и лишь триумфальный успех небесной механики в XVIII веке заставил физиков временно примириться с ньютоновской теорией. Физические основы тяготения прояснились только спустя более чем два века, с появлением Общей теории относительности.
Математический аппарат и общую структуру книги Ньютон построил максимально близкими к тогдашнему стандарту научной строгости — «Началам» Евклида. Математический анализ он сознательно почти нигде не использовал — применение новых, непривычных методов поставило бы под угрозу доверие к изложенным результатам. Эта осторожность, однако, обесценила ньютоновский метод изложения для следующих поколений читателей. Книга Ньютона была первой работой по новой физике и одновременно одним из последних серьёзных трудов, использующих старые методы математического исследования. Все последователи Ньютона уже использовали созданные им мощные методы математического анализа. Крупнейшими непосредственными продолжателями дела Ньютона стали Д’Аламбер, Эйлер, Лаплас, Клеро и Лагранж.
При жизни автора книга выдержала три издания, причём при каждом переиздании автор вносил в книгу существенные дополнения и уточнения[31].
Административная деятельность (1687—1703)[]
1687 год ознаменовался не только выходом великой книги, но и конфликтом Ньютона с королём Яковом II. В феврале король, последовательно проводя свою линию на реставрацию католицизма в Англии, предписал Кембриджскому университету дать степень магистра католическому монаху Альбану Френсису. Руководство университета колебалось, не желая ни нарушать закон, ни раздражать короля; вскоре делегацию учёных, в том числе Ньютона, вызвали для расправы к известному своей грубостью и жестокостью Лорду-верховному судье Джорджу Джеффрису (англ. George Jeffreys). Ньютон выступил против всякого компромисса, ущемляющего университетскую автономию, и убедил делегацию занять принципиальную позицию. В итоге вице-канцлера университета отстранили от должности, но желание короля так и не было исполнено[32]. В одном из писем этих лет Ньютон изложил свои политические принципы[32]:
Всякий честный человек по законам Божеским и человеческим обязан повиноваться законным приказаниям короля. Но если Его Величеству советуют потребовать нечто такое, чего нельзя сделать по закону, то никто не должен пострадать, если пренебрежёт таким требованием.
В 1689 году, после свержения короля Якова II, Ньютон был в первый раз избран в парламент от Кембриджского университета и заседал там немногим более года. Второе избрание состоялось в 1701—1702 годах. Существует популярный анекдот о том, что он взял слово для выступления в палате общин только один раз, попросив закрыть окно во избежание сквозняка. На самом деле, Ньютон выполнял свои парламентские обязанности с той же добросовестностью, с какой он относился ко всем своим делам[33].
Около 1691 года Ньютон серьёзно заболел (скорее всего, отравился в ходе химических опытов[34], хотя имеются и другие версии — переутомление, потрясение после пожара, повлекшего потерю важных результатов, и возрастные недуги[35]). Близкие опасались за его рассудок; несколько сохранившихся его писем этого периода действительно свидетельствуют о душевном расстройстве. Только в конце 1693 года здоровье Ньютона полностью восстановилось[35].
В 1679 году Ньютон познакомился в Тринити с 18-летним аристократом, любителем науки и алхимии, Чарльзом Монтегю (1661—1715). Вероятно, Ньютон произвёл на Монтегю сильнейшее впечатление, потому что в 1696 году, став лордом Галифаксом, президентом Королевского общества и канцлером Казначейства (то есть министром финансов Англии), Монтегю предложил королю назначить Ньютона смотрителем Монетного двора. Король дал своё согласие, и в 1696 году Ньютон занял эту должность, покинул Кембридж и переехал в Лондон. С 1699 года он стал управляющим («мастером») Монетного двора[36].
Для начала Ньютон досконально изучил технологию монетного производства, привёл в порядок документооборот, переделал учёт за последние 30 лет. Одновременно Ньютон энергично и квалифицированно содействовал проводимой Монтегю денежной реформе, восстановив доверие к основательно запущенной его предшественниками монетной системе Англии[37]. В Англии этих лет имели хождение почти исключительно неполновесные, а в немалом количестве и фальшивые монеты. Широкое распространение получила обрезка краёв серебряных монет[38]. Теперь же монету начали производить на специальных станках и по ободку их шла надпись, так что преступное стачивание металла стало практически невозможным. Старая, неполновесная серебряная монета за 2 года была полностью изъята из обращения и перечеканена, выпуск новых монет увеличился, чтобы успевать за потребностью в них, качество их улучшилось. Ранее во время подобных реформ старые деньги население должно было менять по весу, после этого объём наличности уменьшался как у лиц (частных и юридических), так и во всей стране, но проценты и обязательства по кредитам оставались прежними, из-за чего в экономике начиналась стагнация. Ньютон же предложил обменивать деньги по номиналу, что предотвращало указанные проблемы, а неизбежный после такого дефицит средств восполнялся взятием кредитов у других стран (больше всего — у Нидерландов), инфляция резко снизилась[39][36], но внешний государственный долг вырос к середине века до беспрецедентных в истории Англии размеров. Но на протяжении этого времени происходил заметный экономический рост, из-за него выросли налоговые отчисления в казну (сравнявшиеся по размеру с французскими, несмотря на то, что Францию населяло в 2,5 раза больше людей), за счёт этого госдолг постепенно выплачивался[40].
Однако честный и компетентный человек во главе Монетного двора устраивал не всех. С первых же дней на Ньютона посыпались жалобы и доносы, постоянно появлялись комиссии по проверке. Как выяснилось, многие доносы поступали от фальшивомонетчиков, раздражённых ньютоновскими реформами[41]. Ньютон, как правило, равнодушно относился к злословию, но никогда не прощал, если оно затрагивало его честь и репутацию. Он лично участвовал в десятках расследований, и более 100 фальшивомонетчиков были выслежены и осуждены; при отсутствии отягчающих обстоятельств их чаще всего высылали в североамериканские колонии, но несколько главарей были казнены. Число фальшивых монет в Англии значительно сократилось[41]. Монтегю в своих мемуарах высоко оценил незаурядные способности администратора, проявленные Ньютоном и обеспечившие успех реформы[38]. Таким образом, проведённые учёным реформы не только предотвратили экономический кризис, но и через десятилетия привели к значительному росту благосостояния страны.
В апреле 1698 года Монетный двор в ходе «Великого посольства» трижды посетил русский царь Пётр I[38]; к сожалению, подробности его визита и общения с Ньютоном не сохранились. Известно, однако, что в 1700 году в России была проведена монетная реформа, сходная с английской. А в 1713 году первые шесть печатных экземпляров 2-го издания «Начал» Ньютон выслал царю Петру в Россию[42].
Символом научного триумфа Ньютона стали два события 1699 года: началось преподавание системы мира Ньютона в Кембридже (с 1704 года — и в Оксфорде), а Парижская академия наук, оплот его оппонентов-картезианцев, избрала его своим иностранным членом. Всё это время Ньютон ещё числился членом и профессором Тринити-колледжа, но в декабре 1701 года он официально ушёл в отставку со всех своих постов в Кембридже.
В 1703 году скончался президент Королевского общества лорд Джон Сомерс, за 5 лет своего президентства посетивший заседания Общества лишь дважды. В ноябре Ньютон был избран его преемником и управлял Обществом до конца жизни — более двадцати лет. В отличие от своих предшественников, он лично присутствовал на всех заседаниях и сделал всё для того, чтобы британское Королевское общество заняло почётное место в научном мире. Число членов Общества росло (среди них, кроме Галлея, можно выделить Дени Папена, Абрахама де Муавра, Роджера Котса, Брука Тейлора), проводились и обсуждались интересные эксперименты, качество журнальных статей значительно улучшилось, финансовые проблемы были смягчены. Общество обзавелось платными секретарями и собственной резиденцией (на Флит-стрит), расходы на переезд Ньютон оплатил из своего кармана[43]. В эти годы Ньютона часто приглашали в качестве консультанта в различные правительственные комиссии, а принцесса Каролина, будущая королева Великобритании, часами вела с ним во дворце беседы на философские и религиозные темы[44].
Последние годы[]

В 1704 году вышла в свет (сначала на английском языке) монография «Оптика», определявшая развитие этой науки до начала XIX века. Она содержала приложение «О квадратуре кривых» — первое и довольно полное изложение ньютоновской версии математического анализа. Фактически это последний труд Ньютона по естественным наукам, хотя он прожил ещё более 20 лет. Каталог оставленной им библиотеки содержал книги в основном по истории и теологии, и именно этим занятиям Ньютон посвятил остаток жизни[45]. Ньютон оставался управителем Монетного двора, поскольку этот пост, в отличие от должности смотрителя, не требовал от него особой активности. Дважды в неделю он ездил на Монетный двор, раз в неделю — на заседание Королевского общества. Ньютон так никогда и не совершил путешествия за пределы Англии.
В 1705 году королева Анна возвела Ньютона в рыцарское достоинство. Отныне он сэр Исаак Ньютон. Впервые в английской истории звание рыцаря было присвоено за научные заслуги; в следующий раз это произошло более чем век спустя (1819, в отношении Хемфри Дэви)[38]. Впрочем, часть биографов считает, что королева руководствовалась не научными, а политическими мотивами[46]. Ньютон обзавёлся собственным гербом и не очень достоверной родословной.
В 1707 году вышел сборник лекций Ньютона по алгебре, получивший название «Универсальная арифметика». Приведенные в ней численные методы ознаменовали рождение новой перспективной дисциплины — численного анализа.

Могила Ньютона в Вестминстерском аббатстве
В 1708 году начался открытый приоритетный спор с Лейбницем (см. ниже), в который были вовлечены даже царствующие особы. Эта распря двух гениев дорого обошлась науке — английская математическая школа вскоре снизила активность на целый век[47], а европейская — проигнорировала многие выдающиеся идеи Ньютона, переоткрыв их много позднее[37]. Конфликт не погасила даже смерть Лейбница (1716).
Первое издание «Начал» Ньютона давно было раскуплено. Многолетний труд Ньютона по подготовке 2-го издания, уточнённого и дополненного, увенчался успехом в 1710 году, когда вышел первый том нового издания (последний, третий — в 1713 году). Начальный тираж (700 экземпляров) оказался явно недостаточным, в 1714 и 1723 годах была допечатка. При доработке второго тома Ньютону, в виде исключения, пришлось вернуться к физике, чтобы объяснить расхождение теории с опытными данными, и он сразу же совершил крупное открытие — гидродинамическое сжатие струи[48]. Теперь теория хорошо согласовывалась с экспериментом. Ньютон добавил в конец книги «Поучение» с уничтожающей критикой «теории вихрей», с помощью которой его оппоненты-картезианцы пытались объяснить движение планет. На естественный вопрос «а как на самом деле?» в книге следует знаменитый и честный ответ: «Причину… свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не измышляю»[49].
В апреле 1714 года Ньютон обобщил свой опыт финансового регулирования и передал в казначейство свою статью «Наблюдения относительно ценности золота и серебра». В статье содержались конкретные предложения по корректировке стоимости драгоценных металлов. Эти предложения были частично приняты, и это благоприятно сказалось на английской экономике[50].
Негодующих вкладчиков Компании Южных морей сатирически запечатлел Эдвард Мэтью Уорд
Незадолго до смерти Ньютон стал одной из жертв финансовой аферы крупной торговой «Компании Южных морей», пользовавшейся поддержкой правительства. Он приобрёл на крупную сумму ценные бумаги компании, а также настоял на их приобретении Королевским обществом. 24 сентября 1720 года банк компании объявил себя банкротом. Племянница Кэтрин вспоминала в своих записках, что Ньютон потерял более 20000 фунтов, после чего заявил, что может рассчитать движение небесных тел, но не степень безумия толпы. Впрочем, многие биографы полагают, что Кэтрин имела в виду не реальную потерю, а неполучение ожидаемой прибыли[51]. После банкротства компании Ньютон предложил Королевскому обществу компенсировать потери из своего кармана, но его предложение было отклонено[52].
Последние годы жизни Ньютон посвятил написанию «Хронологии древних царств», которой занимался около 40 лет, а также подготовкой третьего издания «Начал», которое вышло в 1726 году. В отличие от второго, изменения в третьем издании были невелики — в основном результаты новых астрономических наблюдений, включая довольно полный справочник по кометам, наблюдавшимся с XIV века. Среди прочих была представлена рассчитанная орбита кометы Галлея, новое появление которой в указанное время (1758 год) наглядно подтвердило теоретические расчёты (к тому времени уже покойных) Ньютона и Галлея. Тираж книги для научного издания тех лет мог считаться огромным: 1250 экземпляров.
В 1725 году здоровье Ньютона начало заметно ухудшаться, и он переселился в Кенсингтон неподалёку от Лондона, где и скончался ночью, во сне, 20 (31) марта 1727 года. Письменного завещания он не оставил, но значительную часть своего крупного состояния он незадолго до смерти передал ближайшим родственникам[53]. Похоронен в Вестминстерском аббатстве[54].
Личные качества[]
Черты характера[]
Составить психологический портрет Ньютона трудно, так как даже симпатизирующие ему люди нередко приписывают Ньютону различные качества[55]. Приходится учитывать и культ Ньютона в Англии, заставлявший авторов воспоминаний наделять великого учёного всеми мыслимыми добродетелями, игнорируя реальные противоречия в его натуре. Кроме того, к концу жизни в характере Ньютона появились такие черты, как добродушие, снисходительность и общительность, ранее ему не свойственные[56].
Внешне Ньютон был невысок, крепкого телосложения, с волнистыми волосами. Он почти не болел, до старости сохранил густые волосы (уже с 40 лет совершенно седые[13]) и все зубы, кроме одного. Никогда (по другим сведениям, почти никогда) не пользовался очками[55], хотя был немного близорук. Почти никогда не смеялся и не раздражался, нет упоминаний о его шутках или иных проявлениях чувства юмора. В денежных расчётах был аккуратен и бережлив, но не скуп. Никогда не был женат. Обычно находился в состоянии глубокой внутренней сосредоточенности, из-за чего нередко проявлял рассеянность: например, однажды, пригласив гостей, он пошёл в кладовую за вином, но тут его осенила какая-то научная идея, он помчался в кабинет и к гостям уже не вернулся. Был равнодушен к спорту, музыке, искусству, театру, путешествиям[57], хотя хорошо умел рисовать[58]. Его помощник вспоминал: «Он не позволял себе никакого отдыха и передышки… считал потерянным всякий час, не посвящённый занятиям [наукой]… Думаю, его немало печалила необходимость тратить время на еду и сон.»[13] Со всем сказанным Ньютон сумел соединить житейскую практичность и здравомыслие, ярко проявившиеся в его успешном управлении Монетным двором и Королевским обществом.
Воспитанный в пуританских традициях, Ньютон установил для себя ряд жёстких принципов и самоограничений[59]. И он не склонен был прощать другим то, что не простил бы себе; в этом корни многих его конфликтов (см. ниже). Тепло относился к родственникам и многим коллегам, но близких друзей не имел[58], не искал общества других людей, держался отстранённо[60]. Вместе с тем Ньютон не был бессердечным и равнодушным к чужой судьбе. Когда после смерти его сводной сестры Анны её дети остались без средств к существованию, Ньютон назначил несовершеннолетним детям пособие, а позже дочь Анны, Кэтрин, взял к себе на воспитание. Постоянно помогал и другим родственникам. «Будучи экономным и расчётливым, он вместе с тем очень свободно обращался с деньгами и был всегда готов помочь другу в нужде, не проявляя при этом навязчивости. Особенно благороден он по отношению к молодёжи»[61]. Многие известные английские учёные — Стирлинг, Маклорен, астроном Джеймс Паунд и другие — с глубокой благодарностью вспоминали помощь, оказанную Ньютоном в начале их научной карьеры[62].
Конфликты[]
Ньютон и Гук[]
Роберт Гук. Реконструкция внешности по словесным описаниям современников.
В 1675 году Ньютон прислал Обществу свой трактат с новыми исследованиями и рассуждениями о природе света. Роберт Гук на заседании заявил, что всё, что есть ценного в трактате, уже имеется в ранее опубликованной книге Гука «Микрография». В частных беседах он обвинял Ньютона в плагиате[63]: «Я показал, что господин Ньютон использовал мои гипотезы об импульсах и волнах» (из дневника Гука). Гук оспаривал приоритет всех открытий Ньютона в области оптики, кроме тех, с которыми он был не согласен[64]. Ольденбург тут же известил Ньютона об этих обвинениях, и тот расценил их как инсинуации. На этот раз конфликт удалось погасить, и учёные обменялись примирительными письмами (1676). Однако с этого момента и вплоть до смерти Гука (1703) Ньютон никаких работ по оптике не публиковал, хотя у него накопился огромный материал, систематизированный им в классической монографии «Оптика» (1704).
Другой приоритетный спор был связан с открытием закона тяготения. Ещё в 1666 году Гук пришел к выводу, что движение планет есть суперпозиция падения на Солнце благодаря силе притяжения к Солнцу, и движения по инерции по касательной к траектории планеты. По его мнению, эта суперпозиция движения и обусловливает эллиптическую форму траектории планеты вокруг Солнца[65]. Однако доказать это математически он не смог и послал в 1679 году Ньютону письмо, где предложил сотрудничество по решению этой задачи. В этом письме было также изложено предположение об убывании силы притяжения к Солнцу обратно пропорционально квадрату расстояния[66]. В ответ Ньютон заметил, что ранее занимался проблемой движения планет, но оставил эти занятия. Действительно, как показывают найденные впоследствии документы, Ньютон занимался проблемой движения планет ещё в 1665—1669 гг., когда он на основании III закона Кеплера установил, что «стремление планет удалиться от Солнца будет обратно пропорционально квадратам их расстояний от Солнца»[67]. Однако представление об орбите планеты как исключительно результате равенства сил притяжения к Солнцу и центробежной силы у него до конца в те годы ещё не выработалось[67][68].
Впоследствии переписка между Гуком и Ньютоном прервалась. Гук вернулся к попыткам построения траектории планеты под действием силы, убывающей по закону обратных квадратов. Однако эти попытки также оказались безуспешными. Между тем, Ньютон вернулся к изучению движения планет и решил эту задачу.
Когда Ньютон готовил к публикации свои «Начала», Гук потребовал, чтобы Ньютон в предисловии оговорил приоритет Гука относительно закона тяготения. Ньютон возразил, что Буллиальд, Кристофер Рен и сам Ньютон пришли к той же формуле независимо и раньше Гука[69]. Разгорелся конфликт, немало отравивший жизнь обоим учёным.
Современные авторы отдают должное и Ньютону, и Гуку. Приоритет Гука заключается в постановке задачи о построении траектории планеты благодаря суперпозиции её падения на Солнце по закону обратных квадратов и движения по инерции. Возможно также, что именно письмо Гука непосредственно подтолкнуло Ньютона завершить решение этой задачи. Однако сам Гук задачу не решил, а также не догадался об универсальности гравитации[70][71]. По словам С. И. Вавилова[13],
Если связать в одно все предположения и мысли Гука о движении планет и тяготении, высказанные им в течение почти 20 лет, то мы встретим почти все главные выводы «Начал» Ньютона, только высказанные в неуверенной и мало доказательной форме. Не решая задачи, Гук нашел её ответ. Вместе с тем перед нами вовсе не случайно брошенная мысль, но несомненно плод долголетней работы. У Гука была гениальная догадка физика-экспериментатора, прозревающего в лабиринте фактов истинные соотношения и законы природы. С подобной редкостной интуицией экспериментатора мы встречаемся в истории науки ещё у Фарадея, но Гук и Фарадей не были математиками. Их дело было довершено Ньютоном и Максвеллом. Бесцельная борьба с Ньютоном за приоритет набросила тень на славное имя Гука, но истории пора, спустя почти три века, отдать должное каждому. Гук не мог идти прямой, безукоризненной дорогой «Математических начал» Ньютона, но своими окольными тропинками, следов которых нам теперь уже не найти, он пришел туда же.
В дальнейшем отношения Ньютона с Гуком оставались напряжёнными. Например, когда Ньютон представил Обществу придуманную им новую конструкцию секстанта, Гук тут же заявил, что изобрёл такой прибор более 30 лет назад (хотя никогда секстантов не строил)[72]. Всё же Ньютон сознавал научную ценность открытий Гука и в своей «Оптике» несколько раз упомянул своего, уже покойного, оппонента[73].
Помимо Ньютона, Гук вёл приоритетные споры со многими другими английскими и континентальными учёными, в том числе с Робертом Бойлем, которого он обвинил в присвоении усовершенствования воздушного насоса, а также с секретарём Королевского общества Ольденбургом, заявив, что с помощью Ольденбурга Гюйгенс украл у Гука идею часов со спиральной пружиной[74].
Миф о том, что Ньютон якобы велел уничтожить единственный портрет Гука, рассматривается ниже.
Ньютон и Флемстид[]
Джон Флемстид.
Джон Флемстид, выдающийся английский астроном, познакомился с Ньютоном в Кембридже (1670), когда Флемстид был ещё студентом, а Ньютон — магистром. Однако уже в 1673 году, почти одновременно с Ньютоном, Флемстид тоже стал знаменит — он опубликовал великолепные по качеству астрономические таблицы, за которые король удостоил его личной аудиенции и звания «Королевский астроном». Более того, король распорядился построить в Гринвиче вблизи Лондона обсерваторию и передать её в распоряжение Флемстида. Однако деньги на оснащение обсерватории король посчитал излишними тратами, и почти все доходы Флемстида уходили на постройку инструментов и хозяйственные нужды обсерватории[75].
Поначалу отношения Ньютона и Флемстида были добросердечными. Ньютон готовил второе издание «Начал» и крайне нуждался в точных наблюдениях Луны для построения и (как он надеялся) подтверждения своей теории её движения; в первом издании теория движения Луны и комет была неудовлетворительна. Это было важно и для утверждения ньютоновской теории тяготения, подвергавшейся на континенте резкой критике картезианцев. Флемстид охотно передавал ему запрошенные данные, и в 1694 году Ньютон с гордостью известил Флемстида, что сравнение расчётных и опытных данных показало их практическое совпадение. В некоторых письмах Флемстид настоятельно просил Ньютона в случае использования наблюдений оговорить его, Флемстида, приоритет; это в первую очередь относилось к Галлею, которого Флемстид не любил и подозревал в научной нечестности, но могло означать и недоверие к самому Ньютону. В письмах Флемстида начинает сквозить обида[75]:
Я согласен: проволока дороже, чем золото, из которого она сделана. Я, однако, собирал это золото, очищал и промывал его, и не смею думать, что Вы столь мало цените мою помощь только потому, что столь легко её получили.
Начало открытому конфликту положило письмо Флемстида, в котором он с извинениями сообщал, что обнаружил в части предоставленных Ньютону данных ряд систематических ошибок. Это ставило под угрозу ньютоновскую теорию Луны и вынуждало переделать расчёты, причём доверие к остальным данным также было поколеблено. Ньютон, который терпеть не мог недобросовестности, был крайне раздражён и даже заподозрил, что ошибки были внесены Флемстидом сознательно[76].
В 1704 году Ньютон посетил Флемстида, который к этому времени получил новые, чрезвычайно точные данные наблюдений, и просил его передать эти данные; взамен Ньютон обещал помочь Флемстиду в издании его основного труда — Большого звёздного каталога. Флемстид, однако, стал тянуть время по двум причинам: каталог был ещё не вполне готов, а Ньютону он больше не доверял и боялся кражи своих бесценных наблюдений. Предоставленных ему для завершения труда опытных вычислителей Флемстид использовал для расчёта положений звёзд, в то время как Ньютона интересовали в первую очередь Луна, планеты и кометы. Наконец, в 1706 году печать книги началась, но Флемстид, страдавший от мучительной подагры и становившийся всё более подозрительным, потребовал, чтобы Ньютон не вскрывал запечатанный типографский экземпляр до окончания печати; Ньютон, которому данные были срочно нужны, пренебрёг этим запретом и выписал нужные величины. Напряжение росло. Флемстид устроил Ньютону скандал за попытку лично внести мелкие корректуры ошибок. Печать книги шла крайне медленно[76].
Из-за финансовых трудностей Флемстид не уплатил членский взнос и был исключён из Королевского общества; новый удар нанесла королева, которая, видимо, по ходатайству Ньютона, передала Обществу контрольные функции над обсерваторией. Ньютон предъявил Флемстиду ультиматум[77]:
Вы представили несовершенный каталог, в котором многого не хватает, Вы не дали положений звёзд, которые были желательны, и я слышал, что печать сейчас остановилась из-за их непредоставления. Таким образом, от Вас ожидается следующее: или Вы пришлёте конец Вашего каталога д-ру Арбетноту, или по крайней мере пришлёте ему данные наблюдений, необходимые для окончания, с тем, чтобы печатание могло продолжаться.
Ньютон также пригрозил, что дальнейшие задержки будут рассматриваться как неподчинение приказу Её Величества. В марте 1710 года Флемстид, после горячих жалоб на несправедливость и козни врагов, всё же передал завершающие листы своего каталога, и в начале 1712 года первый том, под названием «Небесная история», вышел в свет. В нём были все данные, нужные Ньютону, и год спустя переработанное издание «Начал», с гораздо более точной теорией Луны, также не замедлило появиться. Злопамятный Ньютон не включил в издание благодарности Флемстиду и вычеркнул все упоминания о нём, присутствовавшие в первом издании. В ответ Флемстид сжёг все не распроданные 300 экземпляров каталога в своём камине и стал готовить второе его издание, уже по собственному вкусу. В 1719 году он скончался, но усилиями жены и друзей это замечательное издание, гордость английской астрономии, было опубликовано в 1725 году[77].
Преемником Флемстида в королевской обсерватории стал Галлей, который также немедленно засекретил все результаты наблюдений во избежание кражи данных соперниками. До конфликта с Галлеем дело не дошло, однако на заседаниях Общества Ньютон неоднократно отчитывал Галлея за нежелание поделиться нужными Ньютону данными[78].
Ньютон и Лейбниц[]
Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665—1666 годы, однако не публиковал его до 1704 года[79]. Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию, и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это эпохальное открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц.
Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил[80]:
В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимых как для членов рациональных, так и для иррациональных, причем я метод скрыл, переставив буквы следующего предложения: «когда задано уравнение, содержащее любое число текущих количеств, найти флюксии[12] и обратно». Знаменитейший муж отвечал мне, что он также напал на такой метод и сообщил мне свой метод, который оказался едва отличающимся от моего, и то только терминами и начертанием формул.
В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил[81]:
Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потребовал от меня, чтобы я изложил открыто тот метод, который я в то время скрыл от тебя переставлением букв; я сделал это коротко, насколько мог. Надеюсь, что я при этом не написал ничего, что было бы тебе неприятно, если же это случилось, то прошу сообщить, потому что друзья мне дороже математических открытий.
После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704) в журнале Лейбница «Acta eruditorum» появилась анонимная рецензия с оскорбительными намёками в адрес Ньютона. Рецензия ясно указывала, что автором нового исчисления является Лейбниц. Сам Лейбниц решительно отрицал, что рецензия составлена им, но историки сумели найти черновик, написанный его почерком[79]. Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего разгорелась общеевропейская приоритетная война, «наиболее постыдная склока во всей истории математики»[47].
31 января 1713 года Королевское общество получило письмо от Лейбница, содержащее примирительную формулировку: он согласен, что Ньютон пришёл к анализу самостоятельно, «на общих принципах, подобных нашим». Рассерженный Ньютон потребовал создать международную комиссию для прояснения приоритета. Комиссии не понадобилось много времени: спустя полтора месяца, изучив переписку Ньютона с Ольденбургом и другие документы, она единогласно признала приоритет Ньютона, причём в формулировке, на этот раз оскорбительной в отношении Лейбница. Решение комиссии было напечатано в трудах Общества с приложением всех подтверждающих документов. В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида[79]. Друзья Ньютона, со своей стороны, обвинили в плагиате самого Лейбница; по их версии, во время пребывания в Лондоне (1676) Лейбниц в Королевском обществе ознакомился с неопубликованными работами и письмами Ньютона, после чего изложенные там идеи Лейбниц опубликовал и выдал за свои[82].
Война не ослабевала до декабря 1716 года, когда аббат Конти сообщил Ньютону: «Лейбниц умер — диспут окончен»[83].
Научная деятельность[]
С работами Ньютона связана новая эпоха в физике и математике. Он завершил начатое Галилеем создание теоретической физики, основанной, с одной стороны, на опытных данных, а с другой — на количественно-математическом описании природы. В математике появляются мощные аналитические методы. В физике основным методом исследования природы становится построение адекватных математических моделей природных процессов и интенсивное исследование этих моделей с систематическим привлечением всей мощи нового математического аппарата. Последующие века доказали исключительную плодотворность такого подхода.
Философия и научный метод[]
Ньютон решительно отверг популярный в конце XVII века подход Декарта и его последователей-картезианцев, который предписывал при построении научной теории вначале «проницательностью ума» найти «первопричины» исследуемого явления. На практике этот подход часто приводил к выдвижению надуманных гипотез о «субстанциях» и «скрытых свойствах», не поддающихся опытной проверке. Ньютон считал, что в «натуральной философии» (то есть физике) допустимы только такие предположения («принципы», сейчас предпочитают название «законы природы»), которые прямо вытекают из надёжных экспериментов, обобщают их результаты; гипотезами же он называл предположения, недостаточно обоснованные опытами. «Всё…, что не выводится из явлений, должно называться гипотезою; гипотезам же метафизическим, физическим, механическим, скрытым свойствам не место в экспериментальной философии»[29]. Примерами принципов служат закон тяготения и 3 закона механики в «Началах»; слово «принципы» (Principia Mathematica, традиционно переводимое как «математические начала») содержится и в названии его главной книги.
В письме к Пардизу Ньютон сформулировал «золотое правило науки»[84]:
Лучшим и наиболее безопасным методом философствования, как мне кажется, должно быть сначала прилежное исследование свойств вещей и установление этих свойств с помощью экспериментов, а затем постепенное продвижение к гипотезам, объясняющим эти свойства. Гипотезы могут быть полезны лишь при объяснении свойств вещей, но нет необходимости взваливать на них обязанности определять эти свойства вне пределов, выявленных экспериментом… ведь можно изобрести множество гипотез, объясняющих любые новые трудности.
Такой подход не только ставил вне науки умозрительные фантазии (например, рассуждения картезианцев о свойствах «тонких материй», будто бы объясняющих электромагнитные явления), но был более гибким и плодотворным, потому что допускал математическое моделирование явлений, для которых первопричины ещё не обнаружены. Это и произошло с тяготением и теорией света — их природа прояснилась гораздо позже, что не мешало успешному многовековому применению ньютоновских моделей.
Знаменитая фраза «гипотез не измышляю» (лат. Hypotheses non fingo), конечно, не означает, что Ньютон недооценивал важность нахождения «первопричин», если они однозначно подтверждаются на опыте. Полученные из эксперимента общие принципы и следствия из них должны также пройти опытную проверку, которая может привести к корректировке или даже смене принципов[85]. «Вся трудность физики… состоит в том, чтобы по явлениям движения распознать силы природы, а затем по этим силам объяснить остальные явления».
Ньютон, так же как Галилей, полагал, что в основе всех процессов природы лежит механическое движение[49]:
Было бы желательно вывести из начал механики и остальные явления природы… ибо многое заставляет меня предполагать, что все эти явления обусловливаются некоторыми силами, с которыми частицы тел, вследствие причин покуда неизвестных, или стремятся друг к другу и сцепляются в правильные фигуры, или же взаимно отталкиваются и удаляются друг от друга. Так как эти силы неизвестны, то до сих пор попытки философов объяснить явления природы и оставались бесплодными.
Свой научный метод Ньютон сформулировал в книге «Оптика»[86]:
Как в математике, так и при испытании природы, при исследовании трудных вопросов, аналитический метод должен предшествовать синтетическому. Этот анализ заключается в том, что из экспериментов и наблюдений посредством индукции выводят общие заключения и не допускают против них никаких возражений, которые не исходили бы из опытов или других надёжных истин. Ибо гипотезы не рассматриваются в экспериментальной философии. Хотя полученные посредством индукции из экспериментов и наблюдений результаты не могут ещё служить доказательством всеобщих заключений, всё же это — наилучший путь делать заключения, который допускает природа вещей.
В 3-ю книгу «Начал» (начиная со 2-го издания) Ньютон поместил ряд методических правил, направленных против картезианцев; первый из них — вариант «бритвы Оккама»[87]:
Правило I. Не должно принимать в природе иных причин сверх тех, которые истинны и достаточны для объяснения явлений… природа ничего не делает напрасно, а было бы напрасным совершать многим то, что может быть сделано меньшим. Природа проста и не роскошествует излишними причинами вещей…
Правило IV. В опытной физике предложения, выведенные из совершающихся явлений с помощью наведения [индукции], несмотря на возможность противных им предположений, должны быть почитаемы за верные или в точности, или приближённо, пока не обнаружатся такие явления, которыми они ещё более уточняются или же окажутся подверженными исключениям.
Механистические взгляды Ньютона оказались неверны — не все явления природы вытекают из механического движения. Однако его научный метод утвердился в науке. Современная физика успешно исследует и применяет явления, природа которых ещё не выяснена (например, элементарные частицы). Начиная с Ньютона, естествознание развивается, твёрдо уверенное в том, что мир познаваем, потому что природа устроена по простым математическим принципам[88]. Эта уверенность стала философской базой для грандиозного прогресса науки и технологии.
Математика[]
Первые математические открытия Ньютон сделал ещё в студенческие годы: классификация алгебраических кривых 3-го порядка (кривые 2-го порядка исследовал Ферма) и биномиальное разложение произвольной (не обязательно целой) степени, с которого начинается ньютоновская теория бесконечных рядов — нового и мощнейшего инструмента анализа. Разложение в ряд Ньютон считал основным и общим методом анализа функций, и в этом деле достиг вершин мастерства. Он использовал ряды для вычисления таблиц, решения уравнений (в том числе дифференциальных), исследования поведения функций. Ньютон сумел получить разложение для всех стандартных на тот момент функций[21].
Ньютон разработал дифференциальное и интегральное исчисление одновременно с Г. Лейбницем (немного раньше) и независимо от него. До Ньютона действия с бесконечно малыми не были увязаны в единую теорию и носили характер разрозненных остроумных приёмов (см. Метод неделимых). Создание системного математического анализа сводит решение соответствующих задач, в значительной степени, до технического уровня. Появился комплекс понятий, операций и символов, ставший отправной базой дальнейшего развития математики. Следующий, XVIII век, стал веком бурного и чрезвычайно успешного развития аналитических методов.
Возможно, Ньютон пришёл к идее анализа через разностные методы, которыми много и глубоко занимался. Правда, в своих «Началах» Ньютон почти не использовал бесконечно малых, придерживаясь античных (геометрических) приёмов доказательства, но в других трудах применял их свободно[89].
Отправной точкой для дифференциального и интегрального исчисления были работы Кавальери и особенно Ферма, который уже умел (для алгебраических кривых) проводить касательные, находить экстремумы, точки перегиба и кривизну кривой, вычислять площадь её сегмента. Из других предшественников сам Ньютон называл Валлиса, Барроу и шотландского учёного Джеймса Грегори. Понятия функции ещё не было, все кривые он трактовал кинематически как траектории движущейся точки[90].
Уже будучи студентом, Ньютон понял, что дифференцирование и интегрирование — взаимно обратные операции[21]. Эта основная теорема анализа уже более или менее ясно вырисовывалась в работах Торричелли, Грегори и Барроу, однако лишь Ньютон понял, что на этой основе можно получить не только отдельные открытия, но мощное системное исчисление, подобное алгебре, с чёткими правилами и гигантскими возможностями.
Ньютон почти 30 лет не заботился о публикации своего варианта анализа, хотя в письмах (в частности, к Лейбницу) охотно делится многим из достигнутого. Тем временем вариант Лейбница широко и открыто распространяется по Европе с 1676 года. Лишь в 1693 году появляется первое изложение варианта Ньютона — в виде приложения к «Трактату по алгебре» Валлиса[37]. Приходится признать, что терминология и символика Ньютона по сравнению с лейбницевской довольно неуклюжи: флюксия (производная), флюэнта (первообразная), момент величины (дифференциал) и т. п. Сохранились в математике только ньютоновское обозначение «o» для бесконечно малой dt (впрочем, эту букву в том же смысле использовал ранее Грегори), да ещё точка над буквой как символ производной по времени[91].
Достаточно полное изложение принципов анализа Ньютон опубликовал только в работе «О квадратуре кривых» (1704), приложенной к его монографии «Оптика». Почти весь изложенный материал был готов ещё в 1670—1680-е годы, но лишь теперь Грегори и Галлей уговорили Ньютона издать работу, которая, с опозданием на 40 лет, стала первым печатным трудом Ньютона по анализу. Здесь у Ньютона появляются производные высших порядков, найдены значения интегралов разнообразных рациональных и иррациональных функций, приведены примеры решения дифференциальных уравнений 1-го порядка.
В 1707 году вышла книга «Универсальная арифметика». В ней приведены разнообразные численные методы. Ньютон всегда уделял большое внимание приближённому решению уравнений. Знаменитый метод Ньютона позволял находить корни уравнений с немыслимой ранее скоростью и точностью (опубликован в «Алгебре» Валлиса, 1685). Современный вид итерационному методу Ньютона придал Джозеф Рафсон (1690).
В 1711 году наконец был напечатан, спустя 40 лет, «Анализ с помощью уравнений с бесконечным числом членов». В этом труде Ньютон с одинаковой лёгкостью исследует как алгебраические, так и «механические» кривые (циклоиду, квадратрису). Появляются частные производные. В этом же году выходит «Метод разностей», где Ньютон предложил интерполяционную формулу для проведении через (n + 1) данные точки с равноотстоящими или неравноотстоящими абсциссами многочлена n-го порядка. Это разностный аналог формулы Тейлора.
В 1736 году был посмертно издан итоговый труд «Метод флюксий и бесконечных рядов», существенно продвинутый по сравнению с «Анализом с помощью уравнений». В нём приводятся многочисленные примеры отыскания экстремумов, касательных и нормалей, вычисления радиусов и центров кривизны в декартовых и полярных координатах, отыскания точек перегиба и т. п. В этом же сочинении произведены квадратуры и спрямления разнообразных кривых[92].
Надо отметить, что Ньютон не только достаточно полно разработал анализ, но и сделал попытку строго обосновать его принципы. Если Лейбниц склонялся к идее актуальных бесконечно малых, то Ньютон предложил (в «Началах») общую теорию предельных переходов, которую несколько витиевато назвал «метод первых и последних отношений». Используется именно современный термин «предел» (лат. limes), хотя внятное описание сущности этого термина отсутствует, подразумевая интуитивное понимание. Теория пределов изложена в 11 леммах книги I «Начал»; одна лемма есть также в книге II. Арифметика пределов отсутствует, нет доказательства единственности предела, не выявлена его связь с бесконечно малыми. Однако Ньютон справедливо указывает на бо́льшую строгость такого подхода по сравнению с «грубым» методом неделимых. Тем не менее в книге II, введя «моменты» (дифференциалы), Ньютон вновь запутывает дело, фактически рассматривая их как актуальные бесконечно малые[93].
Примечательно, что теорией чисел Ньютон совершенно не интересовался. По всей видимости, физика ему была гораздо ближе математики[94].
Механика[]
Страница «Начал» Ньютона с аксиомами механики
Заслугой Ньютона является решение двух фундаментальных задач.
- Создание для механики аксиоматической основы, которая фактически перевела эту науку в разряд строгих математических теорий.
- Создание динамики, связывающей поведение тела с характеристиками внешних воздействий на него (сил).
Кроме того, Ньютон окончательно похоронил укоренившееся с античных времён представление, что законы движения земных и небесных тел совершенно различны. В его модели мира вся Вселенная подчинена единым законам, допускающим математическую формулировку[95].
Аксиоматика Ньютона состояла из трёх законов, которые сам он сформулировал в следующем виде.
|
Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей. Надо отметить, что Галилей допускал свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений). Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов этот принцип является прямым следствием уравнений динамики (следствие V в «Началах»)[96]. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах»[97].
Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта) и сила. Он ввёл в физику понятие массы как меры инерции и, одновременно, гравитационных свойств. Ранее физики пользовались понятием вес[97], однако вес тела зависит не только от самого тела, но и от его окружения (например, от расстояния до центра Земли), поэтому понадобилась новая, инвариантная характеристика.
Завершили математизацию механики Эйлер и Лагранж.
Всемирное тяготение[]
- (См. также Гравитация, Классическая теория тяготения Ньютона).
Аристотель и его сторонники считали тяжесть стремлением тел «подлунного мира» к их естественным местам. Некоторые другие античные философы (среди них Эмпедокл, Платон) полагали тяжесть стремлением родственных тел к соединению. В XVI веке эту точку зрения поддержал Николай Коперник[98], в гелиоцентрической системе которого Земля считалась лишь одной из планет. Близких взглядов придерживались Джордано Бруно, Галилео Галилей[99]. Иоганн Кеплер считал, что причиной падения тел является не их внутренние стремления, но сила притяжения со стороны Земли, причем не только Земля притягивает камень, но и камень притягивает Землю. По его мнению, сила тяжести распространяется по меньшей мере до Луны[100]. В своих поздних работах он высказывал мнение, что сила тяжести убывает с расстоянием и взаимному притяжению подвержены все тела Солнечной системы[101]. Физическую природу тяжести пытались разгадать Рене Декарт, Жиль Роберваль, Христиан Гюйгенс и другие учёные XVII века[102][103].
Тот же Кеплер первым предположил, что движение планет управляется силами, исходящими от Солнца. В его теории было три таких силы: одна, круговая, подталкивает планету по орбите, действуя по касательной к траектории (за счёт этой силы планета и движется), другая то притягивает, то отталкивает планету от Солнца (за счёт неё орбита планеты является эллипсом) и третья действует поперек плоскости эклиптики (благодаря чему орбита планеты лежит в одной плоскости). Круговую силу он считал убывающей обратно пропорционально расстоянию от Солнца[104]. Ни одна из этих трёх сил не отождествлялась с тяжестью. Кеплерову теорию отверг ведущий астроном-теоретик середины XVII века Исмаэль Буллиальд, по мнению которого, во-первых, планеты движутся вокруг Солнца не под действием исходящих от него сил, а в силу внутреннего стремления, а во-вторых, если бы круговая сила и существовала, она убывала бы обратно второй степени расстояния, а не первой, как считал Кеплер[105]. Декарт полагал, что планеты переносятся вокруг Солнца гигантскими вихрями.
Предположение о существовании исходящей от Солнца силы, управляющей движением планет, высказывал Джереми Хоррокс[106]. По мнению Джованни Альфонсо Борелли, от Солнца исходят три силы: одна продвигает планету по орбите, другая притягивает планету к Солнцу, третья (центробежная), наоборот, отталкивает планету. Эллиптическая орбита планеты является результатом противоборства двух последних[107]. В 1666 г. Роберт Гук высказал предположение, что одной только силы притяжения к Солнцу вполне достаточно для объяснения движения планет, просто нужно предполагать, что планетная орбита является результатом сочетания (суперпозиции) падения на Солнце (благодаря силе притяжения) и движения по инерции (по касательной к траектории планеты). По его мнению, эта суперпозиция движений и обусловливает эллиптическую форму траектории планеты вокруг Солнца. Близкие взгляды, но в достаточно неопределённой форме, высказывал и Кристофер Рен. Гук и Рен догадывались, что сила тяготения убывает обратно пропорционально квадрату расстояния до Солнца[108].
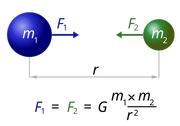
Закон тяготения Ньютона
Однако никто до Ньютона не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера). Более того, именно Ньютон первым догадался, что гравитация действует между двумя любыми телами во Вселенной; движением падающего яблока и вращением Луны вокруг Земли управляет одна и та же сила. Наконец, Ньютон не просто опубликовал предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель:
- закон тяготения;
- закон движения (второй закон Ньютона);
- система методов для математического исследования (математический анализ).
В совокупности эта триада достаточна для полного исследования самых сложных движений небесных тел, тем самым создавая основы небесной механики. Таким образом, только с трудов Ньютона начинается наука динамика, в том числе в применении к движению небесных тел. До создания теории относительности и квантовой механики никаких принципиальных поправок к указанной модели не понадобилось, хотя математический аппарат оказалось необходимым значительно развить.
Первым аргументом в пользу ньютоновской модели послужил строгий вывод на её основе эмпирических законов Кеплера. Следующим шагом стала теория движения комет и Луны, изложенная в «Началах». Позже с помощью ньютоновского тяготения были с высокой точностью объяснены все наблюдаемые движения небесных тел; в этом большая заслуга Эйлера, Клеро и Лапласа, которые разработали для этого теорию возмущений. Фундамент этой теории был заложен ещё Ньютоном, который провёл анализ движения Луны, используя свой обычный метод разложения в ряд; на этом пути он открыл причины известных тогда нерегулярностей (неравенств) в движении Луны.
Закон тяготения позволил решить не только проблемы небесной механики, но и ряд физических и астрофизических задач[109]. Ньютон указал метод определения массы Солнца и планет. Он открыл причину приливов: притяжение Луны (даже Галилей считал приливы центробежным эффектом). Более того, обработав многолетние данные о высоте приливов, он с хорошей точностью вычислил массу Луны. Ещё одним следствием тяготения оказалась прецессия земной оси. Ньютон выяснил, что из-за сплюснутости Земли у полюсов земная ось совершает под действием притяжения Луны и Солнца постоянное медленное смещение с периодом 26000 лет. Тем самым древняя проблема «предварения равноденствий» (впервые отмеченная Гиппархом) нашла научное объяснение[110].
Ньютоновская теория тяготения вызвала многолетние дебаты и критику принятой в ней концепции дальнодействия[111]. Однако выдающиеся успехи небесной механики в XVIII веке утвердили мнение об адекватности ньютоновской модели. Первые наблюдаемые отклонения от теории Ньютона в астрономии (смещение перигелия Меркурия) были обнаружены лишь через 200 лет. Вскоре эти отклонения объяснила общая теория относительности (ОТО); ньютоновская теория оказалась её приближённым вариантом. ОТО также наполнила теорию тяготения физическим содержанием, указав материальный носитель силы притяжения — метрику пространства-времени, и позволила избавиться от дальнодействия[112].
Оптика и теория света[]
Ньютону принадлежат фундаментальные открытия в оптике. Он построил первый зеркальный телескоп (рефлектор), в котором, в отличие от чисто линзовых телескопов, отсутствовала хроматическая аберрация. Он также детально исследовал дисперсию света, показал, что при прохождении белого света через прозрачную призму он разлагается в непрерывный ряд лучей различного цвета вследствие различного преломления лучей разных цветов, тем самым Ньютон заложил основы правильной теории цветов[113]. Ньютон создал математическую теорию открытых Гуком интерференционных колец, которые с тех пор получили название «кольца Ньютона». В письме к Флемстиду он изложил подробную теорию астрономической рефракции[114]. Но его главное достижение — создание основ физической (не только геометрической) оптики как науки[115] и разработка её математической базы, превращение теории света из бессистемного набора фактов в науку с богатым качественным и количественным содержанием, экспериментально хорошо обоснованным[114]. Оптические опыты Ньютона на десятилетия стали образцом глубокого физического исследования[115].
В этот период было множество спекулятивных теорий света и цветности; в основном боролись точка зрения Аристотеля («разные цвета есть смешение света и тьмы в разных пропорциях») и Декарта («разные цвета создаются при вращении световых частиц с разной скоростью»). Гук в своей «Микрографии» (1665) предлагал вариант аристотелевских взглядов. Многие полагали, что цвет есть атрибут не света, а освещённого предмета[116]. Всеобщий разлад усугубил каскад открытий XVII века: дифракция (1665, Гримальди), интерференция (1665, Гук), двойное лучепреломление (1670, Эразм Бартолин, изучено Гюйгенсом), оценка скорости света (1675, Рёмер)[117]. Теории света, совместимой со всеми этими фактами, не существовало.

(опыт Ньютона)
В своём выступлении перед Королевским обществом Ньютон опроверг как Аристотеля, так и Декарта, и убедительно доказал, что белый свет не первичен, а состоит из цветных компонент с разной «степенью преломляемости». Эти-то составляющие и первичны — никакими ухищрениями Ньютон не смог изменить их цвет. Тем самым субъективное ощущение цвета получало прочную объективную базу — в современной терминологии, длину волны света, о которой можно было судить по степени преломления.
В 1689 году Ньютон прекратил публикации в области оптики (хотя продолжал исследования) — по распространённой легенде, поклялся ничего не печатать в этой области при жизни Гука[118]. Во всяком случае, в 1704 году, на следующий год после смерти Гука, выходит в свет (на английском языке) монография «Оптика». В предисловии к ней содержится явный намёк на конфликт с Гуком: «Не желая быть втянутым в диспуты по разным вопросам, я оттягивал это издание и задержал бы его и далее, если бы не настойчивость моих друзей»[119]. При жизни автора «Оптика», как и «Начала», выдержала три издания (1704, 1717, 1721) и множество переводов, в том числе три на латинском языке.
- Книга первая: принципы геометрической оптики, учение о дисперсии света и составе белого цвета с различными приложениями, включая теорию радуги.
- Книга вторая: интерференция света в тонких пластинках.
- Книга третья: дифракция и поляризация света.
Историки выделяют две группы тогдашних гипотез о природе света.
- Эмиссионная (корпускулярная): свет состоит из мелких частиц (корпускул), излучаемых светящимся телом. В пользу этого мнения говорила прямолинейность распространения света, на которой основана геометрическая оптика, однако дифракция и интерференция плохо укладывались в эту теорию.
- Волновая: свет представляет собой волну в невидимом мировом эфире. Оппонентов Ньютона (Гука, Гюйгенса) нередко называют сторонниками волновой теории, однако надо иметь в виду, что под волной они понимали не периодическое колебание, как в современной теории, а одиночный импульс[120]; по этой причине их объяснения световых явлений были мало правдоподобны и не могли составить конкуренцию ньютоновским (Гюйгенс даже пытался опровергнуть дифракцию[73]). Развитая волновая оптика появилась только в начале XIX века.
Ньютона часто считают сторонником корпускулярной теории света; на самом деле он, по своему обыкновению, «гипотез не измышлял»[121] и охотно допускал, что свет может быть связан и с волнами в эфире[122]. В трактате, представленном в Королевское общество в 1675 году, он пишет, что свет не может быть просто колебаниями эфира, так как тогда он, например, мог бы распространяться по изогнутой трубе, как это делает звук. Но, с другой стороны, он предлагает считать, что распространение света возбуждает колебания в эфире, что и порождает дифракцию и другие волновые эффекты[123]. По существу, Ньютон, ясно сознавая достоинства и недостатки обоих подходов, выдвигает компромиссную, корпускулярно-волновую теорию света. В своих работах Ньютон детально описал математическую модель световых явлений, оставляя в стороне вопрос о физическом носителе света: «Учение моё о преломлении света и цветах состоит единственно в установлении некоторых свойств света без всяких гипотез о его происхождении»[122]. Волновая оптика, когда она появилась, не отвергла модели Ньютона, а вобрала их в себя и расширила на новой основе[115].
Несмотря на свою нелюбовь к гипотезам, Ньютон поместил в конце «Оптики» список нерешённых проблем и возможных ответов на них. Впрочем, в эти годы он уже мог себе такое позволить — авторитет Ньютона после «Начал» стал непререкаемым, и докучать ему возражениями уже мало кто решался. Ряд гипотез оказались пророческими. В частности, Ньютон предсказал[73]:
- отклонение света в поле тяготения;
- явление поляризации света;
- взаимопревращение света и вещества.
Другие работы по физике[]
Ньютону принадлежит первый вывод скорости звука в газе, основанный на законе Бойля-Мариотта[124]. Он высказал предположение о существовании закона вязкого трения и описал гидродинамическое сжатие струи[48]. Предложил формулу для закона сопротивления тела в разреженной среде (формула Ньютона)[125][126] и на её основе рассмотрел одну из первых задач о наивыгоднейшей форме обтекаемого тела (аэродинамическая задача Ньютона)[127]. В «Началах» он высказал и аргументировал верное предположение, что комета имеет твёрдое ядро, испарение которого под влиянием солнечного тепла образует обширный хвост, всегда направленный в сторону, противоположную Солнцу[128]. Также Ньютон занимался вопросами теплопередачи, один из результатов носит название закона Ньютона — Рихмана.
Ньютон предсказал сплюснутость Земли у полюсов, оценив её примерно как 1:230. При этом Ньютон использовал для описания Земли модель однородной жидкости, применил закон всемирного тяготения и учёл центробежную силу. Одновременно аналогичные расчёты выполнил Гюйгенс, который не верил в дальнодействующую силу тяготения[129] и подошёл к проблеме чисто кинематически. Соответственно Гюйгенс предсказал более чем вдвое меньшее сжатие, чем Ньютон, 1:576. Более того, Кассини и другие картезианцы доказывали, что Земля не сжата, а вытянута у полюсов наподобие лимона. Впоследствии, хотя и не сразу (первые измерения были неточны), прямые измерения (Клеро, 1743) подтвердили правоту Ньютона; реальное сжатие равно 1:298. Причина отличия этого значения от предложенного Ньютоном в сторону Гюйгенсовского состоит в том, что модель однородной жидкости всё же не вполне точна (плотность заметно возрастает с глубиной)[130]. Более точная теория, явно учитывающая зависимость плотности от глубины, была разработана только в XIX веке.
Ученики[]
Прямых учеников, строго говоря, у Ньютона не было. Однако целое поколение английских учёных выросло на его книгах и в общении с ним, поэтому сами считали себя учениками Ньютона. Среди них наиболее известны:
- Эдмунд Галлей
- Роджер Котс
- Колин Маклорен
- Абрахам де Муавр
- Джеймс Стирлинг
- Брук Тейлор
- Уильям Уистон
Другие сферы деятельности[]
Химия и алхимия[]
«Ньютон» Вильяма Блейка; здесь Ньютон изображен как «божественный геометр».
Параллельно с изысканиями, закладывавшими фундамент нынешней научной (физической и математической) традиции, Ньютон (как и многие его коллеги) много времени отдавал алхимии, а также богословию. Книги по алхимии составляли десятую часть его библиотеки[22]. Никаких трудов по химии или алхимии он не публиковал[131], и единственным известным результатом этого многолетнего увлечения стало серьёзное отравление Ньютона в 1691 году. При эксгумации тела Ньютона в его организме было обнаружено опасное для здоровья содержание ртути[132].
Стьюкли вспоминает, что Ньютон написал трактат по химии, «объясняющий принципы этого таинственного искусства на основании экспериментальных и математических доказательств», но рукопись, к несчастью, сгорела при пожаре, и Ньютон не делал попыток её восстановить. Сохранившиеся письма и заметки наводят на мысль, что Ньютон размышлял над возможностью какого-то объединения законов физики и химии в единую систему мира; несколько гипотез на эту тему он поместил в конце «Оптики»[131].
Б. Г. Кузнецов считает, что алхимические исследования Ньютона были попытками вскрыть атомистическую структуру вещества и других видов материи (например, света, теплоты, магнетизма)[133]:
Был ли Ньютон алхимиком? Он верил в возможность превращения одного металла в другой и в продолжение трёх десятилетий занимался алхимическими исследованиями и изучал алхимические труды средневековья и древности… Сам факт преобладания теоретического интереса и полного отсутствия интереса к получению золота выводит Ньютона за пределы алхимии как элемента средневековой культурной традиции… В основе его атомистики лежит представление об иерархии корпускул, образованной всё менее интенсивными силами взаимного притяжения частей. Эта идея бесконечной иерархии дискретных частиц вещества связана с идеей о единстве материи. Ньютон не верил в существование не способных превращаться друг в друга элементов. Напротив, он предполагал, что представление о неразложимости частиц и соответственно о качественных различиях между элементами связано с исторически ограниченными возможностями экспериментальной техники.
Это предположение подтверждается высказыванием самого Ньютона[22]: «Алхимия имеет дело не с металлами, как полагают невежды. Философия эта — не из тех, что служат тщеславию и обману, она служит скорее пользе и назиданию, притом главное здесь — познание Бога».
Богословие[]
Будучи глубоко верующим человеком, Ньютон рассматривал Библию (как и всё на свете) с рационалистических позиций[134]. С этим подходом, видимо, связано и неприятие Ньютоном Троичности Бога. Большинство историков считает, что Ньютон, много лет трудившийся в Колледже святой Троицы, сам в Троицу не верил[135]. Исследователи его богословских работ обнаружили, что религиозные взгляды Ньютона были близки к еретическому арианству[136] (см. статью Ньютона «Историческое прослеживание двух заметных искажений Священного Писания»).
Степень близости взглядов Ньютона к различным ересям, осуждённым церковью, оценивают по-разному. Немецкий историк Физенмайер предположил, что Ньютон принимал Троицу, но ближе к восточному, православному её пониманию[137]. Американский историк Стивен Снобелен, приведя ряд документальных свидетельств, решительно отверг эту точку зрения и отнёс Ньютона к социнианам[138].
Внешне, однако, Ньютон оставался лояльным государственной англиканской церкви. На то была веская причина: законодательный акт 1698 года «О подавлении богохульства и нечестия» (англ. The Act for the Suppression of Blasphemy and Profaneness) за отрицание любого из лиц Троицы предусматривал поражение в гражданских правах, а при повторении данного преступления — тюремное заключение[44]. К примеру, друг Ньютона Уильям Уистон в 1710 году был лишен профессорского звания и изгнан из Кембриджского университета за свои утверждения о том, что вероисповеданием ранней Церкви было арианство[139]. Однако в письмах единомышленникам (Локк, Галлей и др.) Ньютон был достаточно откровенен.
Кроме антитринитаризма, в религиозном мировоззрении Ньютона усматриваются элементы деизма. Ньютон верил в материальное присутствие Бога в каждой точке Вселенной и называл пространство «чувствилищем Бога» (лат. sensorium Dei)[133]. Эта пантеистическая идея объединяет в единое целое научные, философские и богословские взгляды Ньютона, «все области ньютоновых интересов, от натурфилософии до алхимии, представляют собой различные проекции и одновременно различные контексты этой безраздельно владевшей им центральной идеи»[140].
Ньютон опубликовал (частично) результаты своих теологических исследований в конце жизни, однако начались они гораздо раньше, не позднее 1673 года[141]. Ньютон предложил свой вариант библейской хронологии, оставил работы по библейской герменевтике, написал комментарий на Апокалипсис. Он изучил древнееврейский язык, исследовал Библию по научной методике, привлекая для обоснования своей точки зрения астрономические расчёты, связанные с солнечными затмениями, лингвистический анализ и т. п.[134] По его расчетам, конец света наступит не ранее 2060 года[142].
Теологические рукописи Ньютона ныне хранятся в Иерусалиме, в Национальной Библиотеке[143].
Оценки[]
Надпись на могиле Ньютона гласит[144]:
Здесь покоится сэр Исаак Ньютон, который с почти божественной силой разума первый объяснил с помощью своего математического метода движения и форму планет, пути комет и приливы океанов.
Он был тем, кто исследовал различия световых лучей и проистекающие из них различные свойства цветов, о которых прежде никто и не подозревал. Прилежный, хитроумный и верный истолкователь природы, древности и Святого Писания, он утверждал своей философией величие всемогущего творца, а нравом насаждал требуемую Евангелием простоту.
Да возрадуются смертные, что среди них жило такое украшение рода человеческого.
Оригинальный текст (лат.)H. S. E. ISAACUS NEWTON Eques Auratus,
Qui, animi vi prope divinâ,
Planetarum Motus, Figuras,
Cometarum semitas, Oceanique Aestus. Suâ Mathesi facem praeferente
Primus demonstravit:
Radiorum Lucis dissimilitudines,
Colorumque inde nascentium proprietates,
Quas nemo antea vel suspicatus erat, pervestigavit.
Naturae, Antiquitatis, S. Scripturae,
Sedulus, sagax, fidus Interpres
Dei O. M. Majestatem Philosophiâ asseruit,
Evangelij Simplicitatem Moribus expressit.
Sibi gratulentur Mortales,
Tale tantumque exstitisse
HUMANI GENERIS DECUS.
NAT. XXV DEC. A.D. MDCXLII. OBIIT. XX. MAR. MDCCXXVI.
На статуе, воздвигнутой Ньютону в 1755 г. в Тринити-колледже, высечены стихи из Лукреция[54]:
- Qui genus humanum ingenio superavit (Разумом он превосходил род человеческий)
Сам Ньютон оценивал свои достижения более скромно[135]:
|
Лагранж говорил[145]: «Ньютон был счастливейшим из смертных, ибо существует только одна Вселенная, и Ньютон открыл её законы».
Старорусское произношение фамилии Ньютона — «Невтон». Его вместе с Платоном почтительно упоминает М. В. Ломоносов в своих стихах:
…Может собственных Платонов
и быстрых разумом Невтонов
Российская земля рождать[146].
По словам А. Эйнштейна, «Ньютон был первым, кто попытался сформулировать элементарные законы, которые определяют временной ход широкого класса процессов в природе с высокой степенью полноты и точности» и «… оказал своими трудами глубокое и сильное влияние на всё мировоззрение в целом»[147].
На рубеже 1942—1943 годов, в самые драматические дни Сталинградского сражения, в СССР широко отметили 300-летний юбилей Ньютона. Были выпущены сборник статей и биографическая книга С. И. Вавилова. В знак признательности советскому народу Королевское общество Великобритании подарило Академии наук СССР редчайший экземпляр первого издания ньютоновских «Математических начал» (1687) и черновик письма Ньютона Александру Меншикову, которым последнему сообщалось о избрании его членом Лондонского Королевского Общества[148].
В честь Ньютона названы:
- Единица силы в Международной системе единиц (СИ).
- Кратеры на Луне[149] и на Марсе[150].
- Медаль Исаака Ньютона — международная награда в области физики, ежегодно с 2008 года присуждаемая британским Институтом физики.
- Множество научных законов, теорем и понятий, см. Список объектов, названных в честь Исаака Ньютона.
Мифы[]
Выше уже приводились несколько распространённых легенд: «яблоко Ньютона», его единственное парламентское выступление.
Существует легенда о том, что Ньютон проделал в своей двери два отверстия — одно побольше, другое поменьше, чтобы две его кошки, большая и маленькая, могли самостоятельно заходить в дом. В действительности Ньютон никогда не держал ни кошек, ни других домашних животных[151].
Ещё один миф обвиняет Ньютона в уничтожении единственного портрета Гука, некогда хранившегося в Королевском обществе[152]. В действительности не существует ни единого свидетельства в пользу такого обвинения[153] [154]. Аллан Чепмен, биограф Гука, доказывает, что никакого портрета Гука вообще не существовало (что не удивительно, учитывая дороговизну портретов и постоянные финансовые затруднения Гука). Единственным источником предположения о существовании такого портрета является упоминание посетившего в 1710 году Королевское общество немецкого учёного Захарии фон Уффенбаха о портрете некоего «Хоока» (Hoock), однако Уффенбах не владел английским и, скорее всего, имел в виду портрет другого члена общества, Теодора Хаака (Theodore Haak). Портрет Хаака действительно существовал и сохранился до наших дней. Дополнительным аргументом в пользу мнения, что портрета Гука никогда не было, служит тот факт, что друг Гука и секретарь Общества Ричард Уоллер опубликовал в 1705 году посмертное собрание работ Гука с отличным качеством иллюстраций и подробной биографией, но без портрета Гука; все другие труды Гука также не содержат портрета учёного[153].
Иногда Ньютону приписывают интерес к астрологии. Если он и был, то быстро сменился разочарованием[155][156].
Из факта неожиданного назначения Ньютона управителем Монетного двора некоторые биографы заключают, что Ньютон был членом масонской ложи или иного тайного общества. Однако никаких документальных свидетельств в пользу этой гипотезы не обнаружено[157].
Труды[]
- «Новая теория света и цветов», 1672 (сообщение Королевскому обществу)
- «Движение тел по орбите» (лат. De Motu Corporum in Gyrum), 1684
- «Математические начала натуральной философии» (лат. Philosophiae Naturalis Principia Mathematica), 1687
- «Оптика или трактат об отражениях, преломлениях, изгибаниях и цветах света» (англ. Opticks or a treatise of the reflections, refractions, inflections and colours of light), 1704
- «Универсальная арифметика» (лат. Arithmetica Universalis), 1707
- «Анализ с помощью уравнений с бесконечным числом членов» (лат. De analysi per aequationes numero terminorum infinitas), 1711
- «Метод разностей», 1711
- Труды Исаака Ньютона доступны онлайн
Опубликованы посмертно[]
- «Лекции по оптике» (англ. Optical Lectures), 1728
- «Система мира» (лат. De mundi systemate), 1728
- «Краткая хроника» (англ. A Short Chronicle from the First Memory of Things in Europe, to the Conquest of Persia by Alexander the Great), 1728 (это конспект «Хронологии древних царств», французский перевод чернового варианта был опубликован ещё раньше, в 1725 году)
- «Хронология древних царств» (англ. The Chronology of Ancient Kingdoms), 1728
- «Замечания на книгу пророка Даниила и Апокалипсис св. Иоанна» (англ. Observations Upon the Prophecies of Daniel and the Apocalypse of St. John), 1733, написано около 1690 года
- «Метод флюксий» (лат. Methodus fluxionum, англ. Method of Fluxions), 1736, написан в 1671 году
- «Историческое прослеживание двух заметных искажений Священного Писания» (англ. An Historical Account of Two Notable Corruptions of Scripture), 1754, написано в 1690 году
Канонические издания[]
Классическое полное издание трудов Ньютона в 5 томах на языке оригинала:
- Isaaci Newtoni. Opera quae existant omnia. — Commentariis illustravit Samuel Horsley. — Londini, 1779-1785. (см. ISBN )
Избранная переписка в 7 томах:
- Turnbull, H. W. (Ed.),. The Correspondence of Sir Isaac Newton. — Cambridge: Cambr. Univ. Press, 1959—1977. (см. ISBN )
Переводы на русский язык[]
- Ньютон И. Всеобщая арифметика или Книга об арифметическом синтезе и анализе. — М.: Изд. АН СССР, 1948. — 442 с. — (Классики науки). (см. ISBN )
- Ньютон И. Замечания на книгу пророка Даниила и Апокалипсис св. Иоанна. — Петроград: Новое время, 1915. (см. ISBN )
- Ньютон И. Исправленная хронология древних царств. — М.: РИМИС, 2007. — 656 с. — ISBN 5-9650-0034-0. (см. ISBN )
- Ньютон И. Лекции по оптике. — М.: Изд. АН СССР, 1946. — 298 с. (см. ISBN )
- Ньютон И. Математические начала натуральной философии / Перевод с латинского и примечания А.Н. Крылова. — М.: Наука, 1989. — 688 с. (см. ISBN )
- Ньютон И. Математические работы. — М.-Л.: ОНТИ, 1937. (см. ISBN )
- Ньютон И. Оптика или трактат об отражениях, преломлениях, изгибаниях и цветах света. — М.: Гостехиздат, 1954. (см. ISBN )
См. также[]
- Список объектов, названных в честь Исаака Ньютона
- Историческое прослеживание двух заметных искажений Священного Писания
- Математические начала натуральной философии
Примечания[]
- ↑ Карцев В. П., 1987, Глава «Мать Анна».
- ↑ 2,0 2,1 Акройд П., 2011, Глава 1.
- ↑ Карцев В. П., 1987, с. 8.
- ↑ Акройд П., 2011, Глава 7.
- ↑ 5,0 5,1 Карцев В. П., 1987, с. 43-44, 52-54.
- ↑ Карцев В. П., 1987, с. 49-51.
- ↑ Карцев В. П., 1987, с. 57.
- ↑ Карцев В. П., 1987, с. 69-73.
- ↑ Карцев В. П., 1987, с. 62.
- ↑ 10,0 10,1 10,2 Акройд П., 2011, Глава 3.
- ↑ Спасский Б. И. История физики. — Т. 1. — С. 131. (см. ISBN )
- ↑ 12,0 12,1 Флюксией Ньютон называл производную.
- ↑ 13,0 13,1 13,2 13,3 13,4 Вавилов С. И. Исаак Ньютон. Глава 9. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 96.
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 223. (см. ISBN )
- ↑ Lenta.ru: Прогресс: Недалеко упало.
- ↑ 17,0 17,1 Карцев В. П., 1987, с. 81-82.
- ↑ Карцев В. П., 1987, с. 107, 128.
- ↑ Клайн М. Математика. Поиск истины. — М.: Мир, 1988. — С. 125. (см. ISBN )
- ↑ Акройд П., 2011, Глава 5.
- ↑ 21,0 21,1 21,2 История математики. — Т. 2: Математика XVII столетия. — С. 218. (см. ISBN )
- ↑ 22,0 22,1 22,2 Акройд П., 2011, Глава 4.
- ↑ Карцев В. П., 1987, с. 156-167.
- ↑ Карцев В. П., 1987, с. 128-132.
- ↑ Карцев В. П., 1987, с. 247-248.
- ↑ Карцев В. П., 1987, с. 194-195, 205-206.
- ↑ 27,0 27,1 Карцев В. П., 1987, с. 196-201.
- ↑ «Заглавие книги Ньютона было до известной степени вызовом картезианцам. Воззрения Декарта в окончательном виде изложены в знаменитых „Началах философии“, вышедших в 1644 г. Ньютон, сохраняя для своей книги заглавие Декарта, резко суживает задачу: „Математические начала натуральной философии“» (Вавилов С. И. Исаак Ньютон. Глава 10 (см. ISBN ) ).
- ↑ 29,0 29,1 29,2 Вавилов С. И. Исаак Ньютон. Глава 10. (см. ISBN )
- ↑ Curtis Wilson. The Newtonian achievement in astronomy // R Taton & C Wilson (eds). The General History of Astronomy. — 1989. — Т. 2A.
- ↑ Карцев В. П., 1987, Главы «Второе издание „Начал“» и «Славные времена».
- ↑ 32,0 32,1 Кузнецов Б. Г. Ньютон. — С. 82-86. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 253.
- ↑ Хал Хеллман. Ньютон против Лейбница: Битва титанов. — С. 85. (см. ISBN )
- ↑ 35,0 35,1 Карцев В. П., 1987, с. 254-258.
- ↑ 36,0 36,1 Карцев В. П., 1987, с. 260-270.
- ↑ 37,0 37,1 37,2 История математики. — Т. 2: Математика XVII столетия. — С. 220. (см. ISBN )
- ↑ 38,0 38,1 38,2 38,3 Вавилов С. И. Исаак Ньютон. Глава 14. (см. ISBN )
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 206. (см. ISBN )
- ↑ Д. Баюк. Исаак Ньютон // Энциклопедия для детей. Физика. Т.1 / глав. ред. В. Володин — М: Аванта+, 2000. — С. 131—132.
- ↑ 41,0 41,1 Карцев В. П., 1987, с. 270-276.
- ↑ Карцев В. П., 1987, с. 280-285, 382.
- ↑ Карцев В. П., 1987, с. 306-310, 315-320.
- ↑ 44,0 44,1 Карцев В. П., 1987, с. 353.
- ↑ Карцев В. П., 1987, с. 358.
- ↑ Westfall Richard S. The Life of Isaac Newton. — Cambridge University Press, 1994. — С. 245. — ISBN 0521477379. (см. ISBN )
- ↑ 47,0 47,1 Белл Э. Т. Творцы математики. — С. 97-98. (см. ISBN )
- ↑ 48,0 48,1 Карцев В. П., 1987, с. 372.
- ↑ 49,0 49,1 Ньютон И. Математические начала натуральной философии. — С. 662. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 290-291.
- ↑ Карцев В. П., 1987, с. 391-392.
- ↑ Биржевые игры классиков // Сергей Мануков, Журнал «Деньги» № 31 (788) от 09.08.2010.
- ↑ Карцев В. П., 1987, с. 400-405.
- ↑ 54,0 54,1 Вавилов С. И. Исаак Ньютон. Глава 16. (см. ISBN )
- ↑ 55,0 55,1 Карцев В. П., 1987, с. 6, 393-394, 352.
- ↑ Карцев В. П., 1987, с. 382.
- ↑ Карцев В. П., 1987, с. 350.
- ↑ 58,0 58,1 Вавилов С. И. Исаак Ньютон. Глава 1. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 27.
- ↑ Карцев В. П., 1987, с. 241-242.
- ↑ Белл Э. Т. Творцы математики. — С. 95. (см. ISBN )
- ↑ Карцев В. П., 1987, Глава «Учёные и кораблекрушения».
- ↑ Карцев В. П., 1987, с. 183-188.
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 199. (см. ISBN )
- ↑ Nauenberg M. Robert Hooke’s Seminal Contributions to Orbital Dynamics // Physics in Perspective. — 2005..
- ↑ Кирсанов В. С. Переписка Исаака Ньютона с Робертом Гуком: 1679—80 гг. // Вопросы истории естествознания и техники. — 1996. — № 4. — С. 3-39..
- ↑ 67,0 67,1 Кирсанов В. С. Ранние представления И. Ньютона о тяготении // Вопросы истории естествознания и техники. — 1993. — № 2. — С. 52..
- ↑ Whiteside D. T. Before the Principia: The maturing of Newton's thoughts on dynamical astronomy, 1664—84 // Journal for the History of Astronomy. — 1970..
- ↑ Карцев В. П., 1987, с. 202-207.
- ↑ Nauenberg M. Hooke, Orbital motion, and Newton's Principia // American Journal of Physics. — 1994..
- ↑ Wilson C. Newton's Orbit Problem: A Historian's Response // The College Mathematics Journal. — 1994..
- ↑ Карцев В. П., 1987, с. 305.
- ↑ 73,0 73,1 73,2 Вавилов С. И. Исаак Ньютон. Глава 7. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 171-179.
- ↑ 75,0 75,1 Карцев В. П., 1987, с. 324-327.
- ↑ 76,0 76,1 Карцев В. П., 1987, с. 328-335.
- ↑ 77,0 77,1 Карцев В. П., 1987, с. 336-340.
- ↑ Карцев В. П., 1987, с. 401.
- ↑ 79,0 79,1 79,2 Карцев В. П., 1987, с. 340-348.
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 211. (см. ISBN )
- ↑ Вавилов С. И. Исаак Ньютон. Глава 13. (см. ISBN )
- ↑ Хал Хеллман. Ньютон против Лейбница: Битва титанов. — С. 78. (см. ISBN )
- ↑ Карцев В. П., 1987, Глава «Война философов».
- ↑ Карцев В. П., 1987, с. 160.
- ↑ Ньютон И. Математические начала натуральной философии. — С. 3. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 312.
- ↑ Ньютон И. Математические начала натуральной философии. — С. 502-504. (см. ISBN )
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 72-73. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 224. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 216. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 236-237. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 246-247. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 238-245. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 227. (см. ISBN )
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 71. (см. ISBN )
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 234. (см. ISBN )
- ↑ 97,0 97,1 Спасский Б. И. История физики. — Т. 1. — С. 135-137. (см. ISBN )
- ↑ Knox D. Copernicus’s doctrine of gravity and the natural circular motion of the elements // Journal of the Warburg and Courtauld Institutes. — 2005.
- ↑ Knox D. Bruno’s Doctrine of Gravity, Levity and Natural Circular Motion // Physis, new series. — 2002.
- ↑ Koyre A. The Astronomical Revolution. — New York: Dover, 1973. — P. 193-194. (см. ISBN )
- ↑ Rosen E. (transl. and commentary). Kepler's Somnium. The Dream, or posthumous work on Lunar Astronomy. — Madison, Milwaukee and London, 1967. — P. 217—221. (см. ISBN )
- ↑ Айтон Э. Дж. Картезианская теория тяжести // В кн.: У истоков классической науки. — М.: 1968. — С. 35-63.
- ↑ Фрейман Л. С. Ферма, Торричелли, Роберваль // В кн.: У истоков классической науки. — М.: 1968. — С. 245-247.
- ↑ Stephenson B. Kepler's Physical Astronomy. — Princeton University Press, 1994. (см. ISBN )
- ↑ Wilson C. Predictive astronomy in the century after Kepler // In: Planetary Astronomy from the Renaissance to the Rise of Astrophysics. Part A: Tycho Brahe to Newton. The General History of Astronomy. Volume 2, R. Taton and C. Wilson (eds). — 1989.
- ↑ Wilson C. Predictive astronomy in the century after Kepler // In: Planetary Astronomy from the Renaissance to the Rise of Astrophysics. Part A: Tycho Brahe to Newton. The General History of Astronomy. Volume 2, R. Taton and C. Wilson (eds). — 1989.
- ↑ Черняк В. С. Эволюция творческого мышления в астрономии XVI–XVII вв.: Коперник, Кеплер, Борелли // Философия науки. Вып. 9. — М.: 2003. — С. 17—70.
- ↑ Bennett J. A. Hooke and Wren and the System of the World: Some Points Towards An Historical Account // The British Journal for the History of Science. — 1975.
- ↑ Клайн М. Математика. Поиск истины. — М.: Мир, 1988. — С. 133-134. (см. ISBN )
- ↑ Белл Э. Т. Творцы математики. — С. 96. (см. ISBN )
- ↑ История математики. — Т. 2: Математика XVII столетия. — С. 222. (см. ISBN )
- ↑ Эйнштейн А., Инфельд Л. Эволюция физики. — изд. 2-е. — М.: ГИТТЛ, 1956. — С. 277-281. (см. ISBN )
- ↑ Спасский Б. И. История физики. — Т. 1. — С. 125-128. (см. ISBN )
- ↑ 114,0 114,1 Вавилов С. И. Исаак Ньютон. Глава 8. (см. ISBN )
- ↑ 115,0 115,1 115,2 Мандельштам Л. И. Оптические работы Ньютона. (см. ISBN )
- ↑ Вавилов С. И. Исаак Ньютон. Глава 3. (см. ISBN )
- ↑ Спасский Б. И. История физики. — Т. 1. — С. 122-124. (см. ISBN )
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 217. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 310-311.
- ↑ Кудрявцев П. С. Курс истории физики. — Т. 1. — С. 221. (см. ISBN )
- ↑ «Гипотез не измышляю»
- ↑ 122,0 122,1 Вавилов С. И. Исаак Ньютон. Глава 6. (см. ISBN )
- ↑ Карцев В. П., 1987, с. 179-183.
- ↑ В первом издании «Начал» «Ньютон получил величину скорости звука, значительно меньшую той, которая определялась экспериментально… В последующих изданиях своих „Начал“ (1713, 1725) он указывает возможные причины расхождения… Ньютоновское объяснение расхождения теории с экспериментом было искусственным и не обоснованным достаточно убедительно» (Гельфер Я.М. История и методология термодинамики и статистической физики / 2-е изд. — М.: Высшая школа, 1981. — С. 78-79. — 536 с. (см. ISBN ) ). Правильное выражение для скорости звука было получено Лапласом (Начала, 1989, прим. на стр. 485).
- ↑ Чёрный Г.Г. Газовая динамика. — М.: Наука, 1988. — С. 414. — 424 с. — ISBN 5-02-013814-2. (см. ISBN ) .
- ↑ Формула получила применение в середине XX века в связи с развитием гиперзвуковой аэродинамики (Крайко А.Н. Вариационные задачи газовой динамики. — М.: Наука, 1979. — С. 380. — 448 с. (см. ISBN ) ).
- ↑ Тихомиров В.М. Аэродинамическая задача Ньютона // Квант. — 1982. — № 5. — С. 11-18.
- ↑ Карцев В. П., 1987, с. 388.
- ↑ См. предисловие к книге: Тодхантер И. История математических теорий притяжения и фигуры Земли от Ньютона до Лапласа. М.: 2002.
- ↑ Козенко А. В. Теория фигуры планет // Земля и Вселенная. — 1993. — № 6. — С. 24-29.
- ↑ 131,0 131,1 Вавилов С. И. Исаак Ньютон. Глава 11. (см. ISBN )
- ↑ Weisstein Eric W. Newton, Isaac (1642-1727) (англ.). Проверено 20 ноября 2009. Архивировано из первоисточника 23 августа 2011.
- ↑ 133,0 133,1 Кузнецов Б. Г. Ньютон. — С. 55. (см. ISBN )
- ↑ 134,0 134,1 Кузнецов Б. Г. Ньютон. — С. 104-106. (см. ISBN )
- ↑ 135,0 135,1 История математики. — Т. 2: Математика XVII столетия. — С. 221. (см. ISBN )
- ↑ Вавилов С. И. Исаак Ньютон. Глава 15. (см. ISBN )
- ↑ Pfizenmaier, Thomas C. Was Isaac Newton an Arian? // Journal of the History of Ideas. — 1997. — Т. 58. — № 1.
- ↑ Snobelen, Stephen D. (1999). "Isaac Newton, heretic: the strategies of a Nicodemite" (PDF). British Journal for the History of Science 32: pp. 381–419. doi:10.1017/S0007087499003751.
- ↑ Robert Bruen. William Whiston (англ.). Проверено 7 ноября 2009. Архивировано из первоисточника 23 августа 2011.
- ↑ Дмитриев И. С., 1999, с. 18-19.
- ↑ Акройд П., 2011, Глава 6.
- ↑ Карцев В. П., 1987, Глава «Жизнь в городе».
- ↑ Дмитриев И. С., 1999, с. 12.
- ↑ Селиверстов А. В. Ошибка Исаака Ньютона. Проверено 17 декабря 2013. Архивировано из первоисточника 16 мая 2014.
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 13. (см. ISBN )
- ↑ М. В. Ломоносов «Ода на день восшествия на престол императрицы Елисаветы Петровны, 1747 года»
- ↑ Эйнштейн А. К 200-летию со дня смерти Исаака Ньютона // Собрание научных трудов в четырёх томах. — М.: 2009. — Т. 4. — С. 89.
- ↑ Князев Г. А., Кольцов А. В. Краткий очерк истории Академии наук СССР. Проверено 25 ноября 2009. Архивировано из первоисточника 23 августа 2011.
- ↑ NASA Catalog of Lunar Nomenclature (NASA-RP-1097)
- ↑ Кратер Ньютон
- ↑ Карцев В. П., 1987, с. 248-249.
- ↑ Например, эта легенда преподносится как достоверный факт в книге: Арнольд В. И. Гюйгенс и Барроу, Ньютон и Гук. — М.: Наука, 1989. (см. ISBN ) .
- ↑ 153,0 153,1 Allan Chapman. England's Leonardo: Robert Hooke and the Seventeenth-century Scientific Revolution, Institute of Physics Publishing, 2004. ISBN 0-7503-0987-3: «The 'Hoock' portrait, which the visiting von Uffenbach reported having seen at the Royal Society in 1710, was more likely to have been that of Theodore Haak than of Robert Hooke».
- ↑ Kathy Miles, Charles F. Peters II. Seeing Further, The Legacy of Robert Hooke (англ.). Проверено 18 сентября 2011. Архивировано из первоисточника 4 февраля 2012.
- ↑ Сурдин В. Г. Астрология и наука. Глава "Ньютон и астрология". — М.: Век 2, 2007. — (Наука сегодня). — ISBN 978-5-85099-173-9. (см. ISBN )
- ↑ Robert H. van Gent. Isaac Newton and Astrology (англ.). Проверено 30 августа 2012. Архивировано из первоисточника 16 октября 2012.
- ↑ Bauer, Alain (2007). Isaac Newton's Freemasonary: The Alchemy of Science and Mysticism. Originally published as: Aux origines de la franc-maçonnerie: Newton et les Newtoniens by Editions Dervy (2003): Inner Traditions. Book Excerpt - from Chapter 3. ISBN 1-59477-172-3. http://www.freemasons-freemasonry.com/book_bauer.html. Retrieved 2008-06-25
Комментарии[]
- ↑ Исторически ударение в фамилии Ньютона чаще делалось на втором слоге, хотя английскому оригиналу соответствует ударение на первом, так как ударение в подавляющем большинстве английских двусложных слов падает на начальный слог, если только оно не представляет собой префикс. Современные словари и руководства не имеют единого мнения по поводу правильного ударения в фамилии Ньютон: академический «Философский энциклопедический словарь» (1983) указывает ударение на первом слоге, «Справочник по правописанию, произношению, литературному редактированию» Розенталя (1998) допускает оба варианта ударения, но уточняет: «традиционно — Ньюто́н», «Орфографический словарь» под ред. В. В. Лопатина также допускает вариативность, в БСЭ и в «Орфографическом словаре русского языка» (2010, ISBN 978-5-462-00736-1), утверждённом Приказом Минобрнауки России, указано однозначно ударение Нью́тон.
- ↑ Здесь и далее даты жизни Ньютона приводятся по тогда ещё действовавшему в Англии (до 1752 года) юлианскому календарю. В Великобритании такие даты не пересчитывают по новому стилю.
- ↑ В русских источниках закрепилось произношение Эйскоу, хотя более точно было бы Эскью ([əˈskju]), см. List of names in English with counterintuitive pronunciations.
- ↑ Слово «Начала» в русском переводе названия перекликается с названием труда Евклида, однако в действительности это исторически укоренившийся дефект перевода — в латинском переводе Евклида стоит слово Elementa, а у Ньютона — Principia (принципы).
Литература[]
Биографическая[]
- Акройд П. Исаак Ньютон. Биография. — М.: КоЛибри, Азбука-Аттикус, 2011. — 256 с. — ISBN 978-5-389-01754-2. (см. ISBN )
- Белл Э. Т. Творцы математики. — М.: Просвещение, 1979. — 256 с. (см. ISBN )
- Вавилов С. И. Исаак Ньютон. — 2-е доп. изд. — М.-Л.: Изд. АН СССР, 1945. — 688 с. (см. ISBN )
— Переиздание: — М.: Наука, 1989, с дополнением: Гинзбург В. Л. Несколько замечаний к биографии Исаака Ньютона.
- Кобзарев И. Ю. Ньютон и его время. — М.: Знание, 1978. (см. ISBN )
- Кузнецов Б. Г. Ньютон. — М.: Мысль, 1982. (см. ISBN )
- Хал Хеллман. Ньютон против Лейбница: Битва титанов // Великие противостояния в науке. Десять самых захватывающих диспутов. Глава 3 = Great Feuds in Science: Ten of the Liveliest Disputes Ever. — М.: «Диалектика», 2007. — 320 с. — ISBN 0-471-35066-4. (см. ISBN )
.
- Храмов Ю. А. Ньютон Исаак (Newton Isaac) // Физики: Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — С. 199. — 400 с. — 200 000 экз. (см. ISBN )
(в пер.)
- Christianson G. E. Isaac Newton. Lives and Legacies. — М.: Oxford University Press, 2005. — 144 с. — ISBN 019530070X, 9780195300703. (см. ISBN )
- Westfall R. S. Never at rest: A biog. of Isaac Newton. — Cambridge UP, 1981. (см. ISBN )
- White M. Isaac Newton: The last sorcerer. — Perseus, 1999. — 928 p. — ISBN 5-17-037490-9. (см. ISBN )
Анализ научного творчества[]
- Дмитриев И. С. Неизвестный Ньютон: силуэт на фоне эпохи. — СПб.: Алетейя, 1999. — 784 с. — ISBN 5-89329-156-5. (см. ISBN )
- История математики под редакцией А. П. Юшкевича в трёх томах. — М.: Наука, 1970. — Т. 2. Математика XVII столетия. (см. ISBN )
- Кирсанов В. С. Научная революция XVII века. — М.: Наука, 1987. (см. ISBN )
- Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974. (см. ISBN )
- Мандельштам Л. И. Оптические работы Ньютона // Успехи физических наук. — 1946. — Т. XXVIII. — № 1. — С. 103-129.
- Московский университет — памяти Исаака Ньютона. — М.: МГУ, 1946. (см. ISBN )
- Спасский Б. И. История физики. — Изд. 2-е. — М.: Высшая школа, 1977. — Т. 1. (см. ISBN )
- Хютт В. Ньютон // Философский энциклопедический словарь. — М.: 1983. — С. 443.
- Юшкевич А. П. О математических рукописях Ньютона // Историко-математические исследования. — 1977. — № 22. — С. 127—192.
- Юшкевич А. П. Концепции исчисления бесконечно малых Ньютона и Лейбница // Историко-математические исследования. — 1978. — № 23. — С. 11-31.
- Arthur R. T. W. Newton’s fluxions and equably flowing time // Studies in history and philosophy of science. — 1995. — № 26.
- Bertoloni M. D. Equivalence and priority: Newton versus Leibniz. — Oxford: Clarendon Press, 1993. (см. ISBN )
- Cohen I. B. Newton’s principles of philosophy: inquires into Newton’s scientific work and its general environment. — Cambridge (Mass) UP, 1956. (см. ISBN )
- Cohen I. B. Introduction to Newton’s «Principia». — Cambridge (Mass) UP, 1971. (см. ISBN )
- Snobelen, Stephen D. Isaac Newton, heretic : the strategies of a Nicodemite // British Journal for the History of Science. — 1999. — № 32.
- Lai T. Did Newton renounce infinitesimals? // Historia Mathematica. — 1975. — № 2.
- Selles M. A. Infinitesimals in the foundations of Newton’s mechanics // Historia Mathematica. — 2006. — № 33.
- Weinstock R. Newton’s Principia and inverse-square orbits: the flaw reexamined // Historia Mathematica. — 1992. — № 19.
Художественные произведения[]
- Стивенсон, Нил. Ртуть. — М.: АСТ, 2007. — ISBN 5-17-037490-9. (см. ISBN )
- Керр, Филипп. Знак алхимика: Загадка Исаака Ньютона. — М.: ЭКСМО, 2006. — ISBN 5-699-14944-9. (см. ISBN )
- Егорова, Ирина. Тайный архив Исаака Ньютона. — Санкт-Петербург: Проспект науки, 2009. — ISBN 978-5-903090-29-7. (см. ISBN )
Ссылки[]
- Ахиезер А. И., Белозоров Д. П., Филоненко А. С. Исаак Ньютон: Величие Научного Подвига и Единение Науки. Проверено 21 ноября 2009. Архивировано из первоисточника 23 августа 2011.
- Будрейко Е. Н. Исаак Ньютон и «английское экономическое чудо» (11.09.2009). Проверено 2 ноября 2009. Архивировано из первоисточника 23 августа 2011.
- Работы Isaac Newton в проекте «Гутенберг»
- Sir Isaac Newton (англ.). The MacTutor History of Mathematics archive. Проверено 26 ноября 2009. Архивировано из первоисточника 23 августа 2011.
- Isaac Newton Resources (англ.). Проверено 26 ноября 2009. Архивировано из первоисточника 23 августа 2011.
| Научные и академические посты | ||
|---|---|---|
| Предшественник: Джон Сомерс |
Президент Королевского общества 1703—1727 |
Преемник: Ганс Слоан |
Шаблон:Президенты Королевского общества 1700-х Ошибка Lua в Модуль:External_links на строке 226: attempt to index field 'wikibase' (a nil value).
- Страница 0 - краткая статья
- Страница 1 - энциклопедическая статья
- Разное - на страницах: 2 , 3 , 4 , 5
- Прошу вносить вашу информацию в «Ньютон, Исаак 1», чтобы сохранить ее